题目内容
1.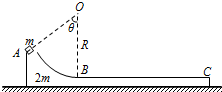 如图所示,静止在光滑水平面上的弧形木板质量为2m,AB部分是半径为R=0.6m、圆心角θ=60°的光滑圆弧轨道,BC部分是长为L=0.75m的粗糙水平轨道.一质量为m的小物块(视为质点)从A处轻轻释放后恰好滑到达C点.重力加速度取g=10m/s2.求:
如图所示,静止在光滑水平面上的弧形木板质量为2m,AB部分是半径为R=0.6m、圆心角θ=60°的光滑圆弧轨道,BC部分是长为L=0.75m的粗糙水平轨道.一质量为m的小物块(视为质点)从A处轻轻释放后恰好滑到达C点.重力加速度取g=10m/s2.求:①物块到达B点时的速度大小υB;
②物块与BC间的动摩擦因数μ.
分析 ①对AB过程和AC过程水平方向列动量守恒的表达式,再对BC过程由能量守恒定律列式求解;
②对系统应用能量守恒定律可以求出动摩擦因数.
解答 解:①物块从A点滑到B点的过程,系统水平方向的动量守恒,以向右为正方向,由动量守恒定律有:
mυB-2mυ1=0,
A到B过程系统机械能能守恒,由机械能守恒定律有:
mg (R-Rcos60°)=$\frac{1}{2}$mυB2+$\frac{1}{2}$×2mυ12,
代入数据解得:υB=2m/s;
②物块从A点滑到C点的过程中,系统动量守恒,以向右为正方向,由动量守恒有:
3 mυ2=0,
由能量守恒定律有:mg (R-Rcos60°)=μmgL
解得:μ=0.4;
答:①物块到达B点时的速度大小υB为2m/s;
②物块与BC间的动摩擦因数μ为0.4.
点评 本题考查动量守恒定律的应用,要注意明确物理过程,合理选择研究对象及过程;由动量守恒定律及能量关系进行分析即可.

练习册系列答案
相关题目
11. 如图所示,A、B两个小球质量为MA、MB,分别连在弹簧两端,B端用平行于斜面的细线固定在倾角为30°的光滑固定斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度大小分别为( )
如图所示,A、B两个小球质量为MA、MB,分别连在弹簧两端,B端用平行于斜面的细线固定在倾角为30°的光滑固定斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度大小分别为( )
 如图所示,A、B两个小球质量为MA、MB,分别连在弹簧两端,B端用平行于斜面的细线固定在倾角为30°的光滑固定斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度大小分别为( )
如图所示,A、B两个小球质量为MA、MB,分别连在弹簧两端,B端用平行于斜面的细线固定在倾角为30°的光滑固定斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度大小分别为( )| A. | $\frac{g}{2}$和$\frac{g}{2}$ | B. | 0和$\frac{g}{2}$ | ||
| C. | $\frac{{{M_A}+{M_B}}}{M_B}•\frac{g}{2}$和0 | D. | 0和$\frac{{{M_A}+{M_B}}}{M_B}•\frac{g}{2}$ |
12. 如图,在负点电荷Q产生的电场中,将两个带等量正电荷的试探电荷q1、q2分别置于A、B两点,虚线为等势线.取无穷远处为零电势点,则下列说法正确的是( )
如图,在负点电荷Q产生的电场中,将两个带等量正电荷的试探电荷q1、q2分别置于A、B两点,虚线为等势线.取无穷远处为零电势点,则下列说法正确的是( )
 如图,在负点电荷Q产生的电场中,将两个带等量正电荷的试探电荷q1、q2分别置于A、B两点,虚线为等势线.取无穷远处为零电势点,则下列说法正确的是( )
如图,在负点电荷Q产生的电场中,将两个带等量正电荷的试探电荷q1、q2分别置于A、B两点,虚线为等势线.取无穷远处为零电势点,则下列说法正确的是( )| A. | A点电势大于B点电势 | |
| B. | A、B两点的电场强度相等 | |
| C. | q1在A点的电势能小于q2在B点的电势能 | |
| D. | 若将q1、q2移动到无穷远的过程中需要外力克服电场力做的功W1<W2 |
5.某质点做匀变速直线运动的位置x与时间t的关系为x=t2+5t+4(式中各物理量均采用国际单位制单位),该质点( )
| A. | 运动的初速度为2m/s | B. | 运动的加速度为1m/s2 | ||
| C. | 在第1s内的位移为6m | D. | 在第1s内的平均速度为2m/s |
9.下列说法正确的是( )
| A. | 一切与热现象有关的宏观自然过程都是不可逆的 | |
| B. | 液晶显示屏是应用液晶的光学各向异性制成的 | |
| C. | 技术成熟后从单一热源吸收热量全部变成有用的功是可能的 | |
| D. | 一定质量的理想气体,温度升高,其内能一定增加 | |
| E. | 分子间的引力随份子距离的增大而增大,分子间的斥力随份子间距离的增大而减小 |
 如图所示,足够长的圆柱形气缸竖直放置,其横截面积为S=1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底L1=12cm,此时气缸内被封闭气体的压强为P1=1.5×105 Pa,温度为T1=300K.外界大气压为P0=1.0×105Pa,g=10m/s2.
如图所示,足够长的圆柱形气缸竖直放置,其横截面积为S=1×10-3m2,气缸内有质量m=2kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底L1=12cm,此时气缸内被封闭气体的压强为P1=1.5×105 Pa,温度为T1=300K.外界大气压为P0=1.0×105Pa,g=10m/s2.
 所受重力G1=8N的砝码悬挂在细绳PA和PB的结点上,PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示(已知sin37°=0.6 cos37°=0.8),求:
所受重力G1=8N的砝码悬挂在细绳PA和PB的结点上,PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示(已知sin37°=0.6 cos37°=0.8),求: