题目内容
如图所示，一质点做平抛运动先后经过A、B两点，到达A点时速度方向与水平方向的夹角为30°，到达B 点时速度方向与水平方向的夹角为60°。
（1）求质点在A、B位置的竖直分速度大小之比；
（2）设质点的位移AB与水平方向的夹角为θ，求tanθ的值。
（1）求质点在A、B位置的竖直分速度大小之比；
（2）设质点的位移AB与水平方向的夹角为θ，求tanθ的值。
解：设质点平抛的初速度为v0，在A、B点的竖直分速度分别为vA、vB，则
vAy=v0tan30°，vBy=v0tan60°，解得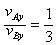
（2）设从A到B时间为t，竖直位移和水平位移分别为y、x，则
联立解得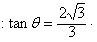
vAy=v0tan30°，vBy=v0tan60°，解得
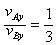
（2）设从A到B时间为t，竖直位移和水平位移分别为y、x，则
联立解得
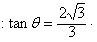
练习册系列答案
相关题目
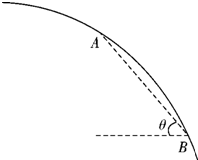（2011?武汉模拟）如图所示，一质点做平抛运动先后经过A、B两点，到达A点时速度方向与水平方向的夹角为30°，到达B点时速度方向与水平方向的夹角为60°．
