题目内容
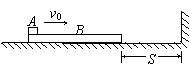
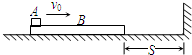 一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为S=0.5m.一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端.
一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为S=0.5m.一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端.设定物体A可视为质点,A、B间的动摩擦因数μ=0.2,B与竖直挡板碰撞时间极短且碰撞过程中无机械能损失,g取10m/s2.求:
(1)B与竖直挡板第一次碰撞前的瞬间,A、B的速度值各是多少?
(2)最后要使A不从B上滑下,木板B的长度至少是多少?(最后结果保留三位有效数字.)
分析:(1)A在B上滑动时,以AB整体为研究对象可知,AB组成的系统动量守恒,由此可以求出AB速度相等时的速度;对B,运用动能定理可求出此过程滑行的位移,即可判断出B与挡板碰撞时,A、B还未达到共同速度.再对系统运用动量守恒和对B运用动能定理分别列式,即可求得B与竖直挡板第一次碰撞前的瞬间A、B的速度值.
(2)B与挡板第一次碰后向左减速运动,由动能定理可求得向左运动的最大距离.在A的作用下B再次反向向右运动,可达到共同速度,由系统的动量守恒求出共同速度.当B第二次与挡板碰撞后,B的速度立即反向,而A将继续向右运动,此后由于系统的总动量向左,最后A、B将以共同速度v3向左匀速运动.再运用动量守恒和能量守恒求出A在B上运动的总路程,就是木板B最小的长度.
(2)B与挡板第一次碰后向左减速运动,由动能定理可求得向左运动的最大距离.在A的作用下B再次反向向右运动,可达到共同速度,由系统的动量守恒求出共同速度.当B第二次与挡板碰撞后,B的速度立即反向,而A将继续向右运动,此后由于系统的总动量向左,最后A、B将以共同速度v3向左匀速运动.再运用动量守恒和能量守恒求出A在B上运动的总路程,就是木板B最小的长度.
解答:解:(1)设A、B达到共同速度为v1时,B向右运动距离为S1
由动量守恒定律有:mv0=(M+m)v1
由动能定理有:μmgS1=
M
联立解得:S1=
=
m=2m
由于S=0.5m<2m,可知B与挡板碰撞时,A、B还未达到共同速度.设B与挡板碰撞前瞬间A的速度为vA,B的速度为vB,则
由动量守恒定律有:mv0=mvA+MvB
由动能定理有:μmgS=
M
联立解得:vA=4m/s、vB=1m/s
(2)B与挡板第一次碰后向左减速运动,当B速度减为零时,B向左运动的距离设为SB,由动能定理有:μmgSB=
M
由上式解得:SB=0.5m
在A的作用下B再次反向向右运动,设当A、B向右运动达到共同速度v2时B向右运动距离为S2,由动量守恒定律有:mvA-MvB=(M+m)v2
由动能定理有:μmgS2=
M
解得:v2=
m/s、S2=
m<SB
故A、B以共同速度
m/s向右运动,B第二次与挡板碰撞后,以原速率反弹向左运动.此后由于系统的总动量向左,故最后A、B将以共同速度v3向左匀速运动.
由动量守恒定律有:(M-m)v2=(M+m)v3
解得:v3=
m/s
设A在B上运动的总量程为L(即木板B的最小长度),由系统功能关系得:μmgL=
m
-
(M+m)
代入数据解得:L=8.96m
答:
(1)B与竖直挡板第一次碰撞前的瞬间,A、B的速度值分别是4m/s、1m/s.
(2)最后要使A不从B上滑下,木板B的长度至少是8.96m.
由动量守恒定律有:mv0=(M+m)v1
由动能定理有:μmgS1=
| 1 |
| 2 |
| v | 2 1 |
联立解得:S1=
| ||||
| μmg |
| ||||
| 0.2×1×10 |
由于S=0.5m<2m,可知B与挡板碰撞时,A、B还未达到共同速度.设B与挡板碰撞前瞬间A的速度为vA,B的速度为vB,则
由动量守恒定律有:mv0=mvA+MvB
由动能定理有:μmgS=
| 1 |
| 2 |
| v | 2 B |
联立解得:vA=4m/s、vB=1m/s
(2)B与挡板第一次碰后向左减速运动,当B速度减为零时,B向左运动的距离设为SB,由动能定理有:μmgSB=
| 1 |
| 2 |
| v | 2 B |
由上式解得:SB=0.5m
在A的作用下B再次反向向右运动,设当A、B向右运动达到共同速度v2时B向右运动距离为S2,由动量守恒定律有:mvA-MvB=(M+m)v2
由动能定理有:μmgS2=
| 1 |
| 2 |
| v | 2 2 |
解得:v2=
| 2 |
| 3 |
| 2 |
| 9 |
故A、B以共同速度
| 2 |
| 3 |
由动量守恒定律有:(M-m)v2=(M+m)v3
解得:v3=
| 2 |
| 9 |
设A在B上运动的总量程为L(即木板B的最小长度),由系统功能关系得:μmgL=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 3 |
代入数据解得:L=8.96m
答:
(1)B与竖直挡板第一次碰撞前的瞬间,A、B的速度值分别是4m/s、1m/s.
(2)最后要使A不从B上滑下,木板B的长度至少是8.96m.
点评:解决本题的关键是A与B组成的系统在碰撞过程中满足动量守恒,B在运动过程中遵循牛顿第二定律,A在B上滑动时,A相对于B滑动的位移为相对位移,摩擦力在相对位移上做的功等于系统机械能的损耗.

练习册系列答案
相关题目

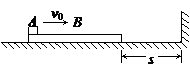 一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为s=0.5m.一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端.设定物体A可视为质点,A、B间的动摩擦因数μ=0.2,B与竖直挡板碰撞时间极短且碰撞过程中无机械能损失,g取10m/s2.求:
一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为s=0.5m.一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端.设定物体A可视为质点,A、B间的动摩擦因数μ=0.2,B与竖直挡板碰撞时间极短且碰撞过程中无机械能损失,g取10m/s2.求: