题目内容
(2013?河南模拟)如图所示,一质量M=2kg的长木板B静止于光滑水平面上,B的右边有竖直墙壁.现有一小物体A(可视为质点)质量m=lkg,以速度v0=6m/s从B的左端水平滑上B,已知A和B间的动摩擦因数μ=0.2,B与竖直墙壁的碰撞时间极短,且碰撞时无机械能损失,若B的右端距墙壁s=4m,要使A最终不脱离B,则木板B的长度至少多长?
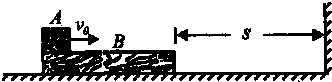

分析:A在B上滑动时,设A滑上B后达到共同速度前并未碰到档板,以AB整体为研究对象可知,AB组成的系统动量守恒,由此可以求出AB速度相等时的速度;根据动能定理求出在这一过程中B的位移,即可判断两者速度相等时B有无碰撞墙壁.若B还碰撞到墙壁,A、B达到共同速度后再匀速向前运动.B碰到竖直挡板后,根据动量守恒定律得A、B最后相对静止时的速度,根据动能定理或能量守恒定律求解,A、B的相对位移,即可得到木板最小长度.
解答:解:设A滑上B后达到共同速度前并未碰到档板,则根据动量守恒定律得它们的共同速度为v,
有mv0=(M+m)v,
代人数据解得:v=2m/s,
在这一过程中,B的位移为sB由动能定理:μmgsB=
Mv2
代人数据解得:sB=2m.
当s=4m时,A、B达到共同速度v=2m/s后再匀速向前运动2m碰到档板,B碰到竖直挡板后,根据动量守恒定律得A、B最后相对静止时的速度为v',则
Mv-mv=(M+m)v',
解得:v′=
m/s.
在这一过程中,A、B的相对位移为s1,根据动能定理,得:μmgs1=
m
-
(M+m)v′2,
解得:s1=8.67m.
因此,A、B最终不脱离的木板最小长度为8.67m.
答:要使A最终不脱离B,则木板B的长度至少为8.67m.
有mv0=(M+m)v,
代人数据解得:v=2m/s,
在这一过程中,B的位移为sB由动能定理:μmgsB=
| 1 |
| 2 |
代人数据解得:sB=2m.
当s=4m时,A、B达到共同速度v=2m/s后再匀速向前运动2m碰到档板,B碰到竖直挡板后,根据动量守恒定律得A、B最后相对静止时的速度为v',则
Mv-mv=(M+m)v',
解得:v′=
| 2 |
| 3 |
在这一过程中,A、B的相对位移为s1,根据动能定理,得:μmgs1=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
解得:s1=8.67m.
因此,A、B最终不脱离的木板最小长度为8.67m.
答:要使A最终不脱离B,则木板B的长度至少为8.67m.
点评:解决本题的关键是A与B组成的系统在碰撞过程中满足动量守恒,A在B上滑动时,A相对于B滑动的位移为相对位移,摩擦力在相对位移上做的功等于系统机械能的损耗.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 (2013?河南模拟)如图所示,质量分别为没m、n的两个物体A,B用一根质量不计的细绳相连接,在恒力F的作用下,在水平面上运动(两物体与水平面之间的动摩擦因数相同),则以下对细绳中的拉力T的说法正确的是( )
(2013?河南模拟)如图所示,质量分别为没m、n的两个物体A,B用一根质量不计的细绳相连接,在恒力F的作用下,在水平面上运动(两物体与水平面之间的动摩擦因数相同),则以下对细绳中的拉力T的说法正确的是( )

 (2013?河南模拟)如图所示,正方形线框的边长为L,电容器的电容为C.正方形线框的一半放在垂直于纸面向里的匀强磁场中,在磁场以变化率k均为减弱的过程中( )
(2013?河南模拟)如图所示,正方形线框的边长为L,电容器的电容为C.正方形线框的一半放在垂直于纸面向里的匀强磁场中,在磁场以变化率k均为减弱的过程中( )