题目内容
【题目】如图所示,A是一面积为S=0.2m2、匝数为n=100匝的圆形线圈,处在均匀磁场中,磁场方向与线圈平面垂直,磁感应强度随时间变化规律为B=(6﹣0.02t)T,开始时外电路开关S断开,已知R1=4Ω,R2=6Ω,电容器电容C=30 μF,线圈内阻不计,求: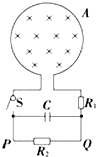
(1)S闭合后,通过R2的电流大小;
(2)S闭合一段时间后又断开,在断开后流过R2的电荷量.
【答案】
(1)解:由法拉第电磁感应定律可得:
E=n ![]() =n
=n ![]() =100×0.02×0.2V=0.4V;
=100×0.02×0.2V=0.4V;
则电路中电流为:
I= ![]() =
= ![]() =0.04A;
=0.04A;
即通过R的电流大小为0.04A;
答:通过R的电流大小为0.04A,
(2)解:由欧姆定律可得R2两端的电压为:
U=IR2=0.04×6=0.24V;
则电容器的电量为:
Q=UC=30×10﹣6×0.24=7.2×10﹣6C;
即电容器的电荷量为7.2×10﹣6C.
因此在断开后流过R2的电荷量为7.2×10﹣6C
答:在断开后流过R2的电荷量为7.2×10﹣6C.
【解析】(1)由法拉第电磁感应定律可得出线圈中的电动势,则由欧姆定律可求得通过R的电流;由楞次定律可求得电流的方向;(2)电容器与R并联,则可求得电容器两端的电压,由电容器的定义,可求得电荷量.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目