题目内容
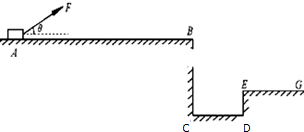
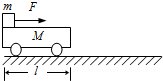
如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为Ff.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )
| A.物块到达小车最右端时具有的动能为F(L+s) |
| B.物块到达小车最右端时,小车具有的动能为Ffs |
| C.物块克服摩擦力所做的功为Ff(L+s) |
| D.物块和小车增加的机械能为Ffs |

A、对物块分析,物块相对于地的位移为L+s,根据动能定理得,(F-Ff)(L+s)=
| 1 |
| 2 |
B、对小车分析,小车对地的位移为l,根据动能定理得,Ffl=
| 1 |
| 2 |
C、物块相对于地的位移大小为L+s,则物块克服摩擦力所做的功为Ff(L+s).故C正确.
D、根据能量守恒得,外力F做的功转化为小车和物块的机械能和摩擦产生的内能,则有:F(L+s)=△E+Q,则物块和小车增加的机械能为△E=F(L+s)-FfL.故D错误.
故选:C.

练习册系列答案
相关题目