题目内容
4. 两个质量均为m的小球,悬于长L的细丝线上.丝线的另一点固定于同一点O.当使两球带上等量同种电荷后,两球互相排斥使两丝线间形成α=90°的夹角.求每个小球的带电量.
两个质量均为m的小球,悬于长L的细丝线上.丝线的另一点固定于同一点O.当使两球带上等量同种电荷后,两球互相排斥使两丝线间形成α=90°的夹角.求每个小球的带电量.
分析 对小球进行受力分析,通过共点力平衡以及库仑定律求出每个小球的电荷量.
解答 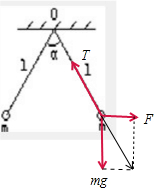 解:设小球在水平方向受到库仑力的大小为F.以右边的小球为研究对象,分析受力如图.
解:设小球在水平方向受到库仑力的大小为F.以右边的小球为研究对象,分析受力如图.
则根据平衡条件有:F=mgtan$\frac{α}{2}$=mgtan45°=$\frac{\sqrt{2}}{2}$mg,
根据库仑定律得:F=k$\frac{{q}^{2}}{{l}^{2}}$,
解得:q=$\sqrt{\frac{\sqrt{2}mg{l}^{2}}{2k}}$.
答:每个小球的带电量为$\sqrt{\frac{\sqrt{2}mg{l}^{2}}{2k}}$.
点评 本题中两边的球是对称的,分析其中一个小球即可得出正确结论;在电场中处理问题的方法与力学是一致的,做好受力分析是解决问题的关键.

练习册系列答案
相关题目
11.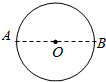 如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )
如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )
 如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )
如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )| A. | 人从A到B的平均速度方向由A指向B | |
| B. | 人从A到B的平均速度方向沿B点的切线方向 | |
| C. | 人在B点的瞬时速度方向由A指向B | |
| D. | 人在B点的瞬时速度方向沿B点的切线方向 |
9. 阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
 阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )| A. | 径迹2的粒子比径迹1的粒子速度大 | |
| B. | 径迹4的粒子与径迹3的粒子在磁场中回旋时间相等 | |
| C. | 3是反α粒子径迹 | |
| D. | 4是反α粒子径迹 |
16.做匀加速直线运动的物体,运动了时间t.在时间t内,以下说法正确的是( )
| A. | 物体的加速度越大,通过的路程一定越长 | |
| B. | 物体的初速度越大,通过的路程一定越长 | |
| C. | 物体的末速度越大,通过的路程一定越长 | |
| D. | 物体的平均速度越大,通过的路程一定越长 |
13.因测试需要,一辆汽车在某雷达测速区沿平直路面从静止开始匀加速一段时间后,又接着做匀减速运动直到最后停止.表中给出了雷达测出的各个时刻对应的汽车速度数值.求:
(1)汽车在运动过程中的最大速度是多少?
(2)汽车在匀加速和匀减速两阶段的加速度a1、a2分别是多少?
(3)汽车在该区域行驶的总位移s是多少?
| 时刻/s | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
| (m•s-2) | 0 | 3.0 | 6.0 | 9.0 | 12.0 | 10.0 | 8.0 | 6.0 | 4.0 | 2.0 | 0 |
(2)汽车在匀加速和匀减速两阶段的加速度a1、a2分别是多少?
(3)汽车在该区域行驶的总位移s是多少?
14. 点电荷Q1、Q2和Q3产生的静电场的等势面与纸面的交线如图中实线所示,图中标在等势面上的数字分别表示该等势面的电势,a、b、c等点表示等势面上的点,下列说法中正确的是( )
点电荷Q1、Q2和Q3产生的静电场的等势面与纸面的交线如图中实线所示,图中标在等势面上的数字分别表示该等势面的电势,a、b、c等点表示等势面上的点,下列说法中正确的是( )
 点电荷Q1、Q2和Q3产生的静电场的等势面与纸面的交线如图中实线所示,图中标在等势面上的数字分别表示该等势面的电势,a、b、c等点表示等势面上的点,下列说法中正确的是( )
点电荷Q1、Q2和Q3产生的静电场的等势面与纸面的交线如图中实线所示,图中标在等势面上的数字分别表示该等势面的电势,a、b、c等点表示等势面上的点,下列说法中正确的是( )| A. | 位于g点的点电荷不受电场力作用 | |
| B. | b点的场强比a点的场强大 | |
| C. | 把电量为q的正点电荷从a点移到i点,再从i点移到f点的过程中,电场力做的总功大于把该点电荷从a点直接移到f点过程中电场力所做的功 | |
| D. | 把电量为1 C的正点电荷从m点移到c点的过程中电势能增加7 kJ |
 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,引力常量为G,自转周期为T,求:
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,引力常量为G,自转周期为T,求: 如图所示,竖直平面内有两个有界区域Ⅰ和Ⅱ,宽度均为L,竖直虚线是它们的分界线.区域Ⅰ中有垂直纸面向里的匀强磁场,区域Ⅱ中有匀强电场.质量为m、电量为q的带正电的粒子(重力不计)以初速度V0从O点沿水平方向射入磁场,运动到P点(图中未标出)离开磁场并进入电场,离开时速度方向与竖直方向成45°角,粒子经一段时间后到达电场右边界时速度恰好为零,此后再次从P点返问磁场.求:
如图所示,竖直平面内有两个有界区域Ⅰ和Ⅱ,宽度均为L,竖直虚线是它们的分界线.区域Ⅰ中有垂直纸面向里的匀强磁场,区域Ⅱ中有匀强电场.质量为m、电量为q的带正电的粒子(重力不计)以初速度V0从O点沿水平方向射入磁场,运动到P点(图中未标出)离开磁场并进入电场,离开时速度方向与竖直方向成45°角,粒子经一段时间后到达电场右边界时速度恰好为零,此后再次从P点返问磁场.求: 用如图所示装置做“研究有固定转动轴物体的平衡条件”的实验,力矩盘上各同心圆的间距相等.
用如图所示装置做“研究有固定转动轴物体的平衡条件”的实验,力矩盘上各同心圆的间距相等.