题目内容
1.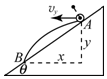 如图所示,从倾角为θ的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,以下说法正确的是( )
如图所示,从倾角为θ的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,以下说法正确的是( )| A. | 从抛出到落在斜面上B点所用时间为$\frac{{2{v_0}sinθ}}{g}$ | |
| B. | 从抛出到落在斜面上B点所用时间为$\frac{{2{v_0}tanθ}}{g}$ | |
| C. | 从抛出到离斜面最远时所用时间为$\frac{{{v_0}sinθ}}{g}$ | |
| D. | 从抛出到离斜面最远时所用时间为$\frac{{{v_0}tanθ}}{g}$ |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合竖直位移与水平位移的关系求出运动的时间.
当小球的速度与斜面平行时,距离斜面最远,结合平行四边形定则求出竖直分速度,根据速度时间公式求出离斜面最远的时间.
解答 解:AB、根据$tanθ=\frac{y}{x}=\frac{\frac{1}{2}g{t}_{\;}^{2}}{{v}_{0}^{\;}t}$
得:t=$\frac{2{v}_{0}^{\;}tanθ}{g}$.故A错误,B正确;
CD、当小球的速度方向与斜面平行时,距离斜面最远.
根据平行四边形定则知,小球此时竖直方向上的分速度vy=v0tanθ.
根据vy=gt得:t=$\frac{{v}_{y}^{\;}}{g}=\frac{{v}_{0}^{\;}tanθ}{g}$.故C错误,D正确;
故选:BD
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道小球速度方向与斜面方向平行时,距离斜面最远.

练习册系列答案
相关题目
10.人以20N的恒力推着小车在粗糙的水平面上前进了5.0m,人放手后,小车还前进了2.0m才停下来,则小车在运动过程中,人的推力所做的功为( )
| A. | 100J | B. | 140J | C. | 60J | D. | 无法确定 |
12.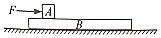 如图所示,在粗糙水平地面上,质量mA=2kg的木块A置于足够长的质量mB=1kg的木板B上,A、B间的动摩擦因数为0.2,B与水平地面间的动摩擦因数为0.1,开始时A、B均处于静止状态,现从t=0时起给A施加一大小为F=2t(N).方向水平向右的力,取重力加速度g=10m/s2,假定最大静摩擦力等于滑动摩擦力,则下列说法中错误的是( )
如图所示,在粗糙水平地面上,质量mA=2kg的木块A置于足够长的质量mB=1kg的木板B上,A、B间的动摩擦因数为0.2,B与水平地面间的动摩擦因数为0.1,开始时A、B均处于静止状态,现从t=0时起给A施加一大小为F=2t(N).方向水平向右的力,取重力加速度g=10m/s2,假定最大静摩擦力等于滑动摩擦力,则下列说法中错误的是( )
 如图所示,在粗糙水平地面上,质量mA=2kg的木块A置于足够长的质量mB=1kg的木板B上,A、B间的动摩擦因数为0.2,B与水平地面间的动摩擦因数为0.1,开始时A、B均处于静止状态,现从t=0时起给A施加一大小为F=2t(N).方向水平向右的力,取重力加速度g=10m/s2,假定最大静摩擦力等于滑动摩擦力,则下列说法中错误的是( )
如图所示,在粗糙水平地面上,质量mA=2kg的木块A置于足够长的质量mB=1kg的木板B上,A、B间的动摩擦因数为0.2,B与水平地面间的动摩擦因数为0.1,开始时A、B均处于静止状态,现从t=0时起给A施加一大小为F=2t(N).方向水平向右的力,取重力加速度g=10m/s2,假定最大静摩擦力等于滑动摩擦力,则下列说法中错误的是( )| A. | t=1.5s时木板B开始相对地面滑动 | B. | 木板B的加速度最大值为1m/s2 | ||
| C. | t=2s时木板相对于木板B开始滑动 | D. | t=3s时木板相对于木板B开始滑动 |
9. 如图所示,细线的一端与一小球相连,另一端悬于固定点O,现使小球绕O点在竖直面内做圆周运动,当小球运动到最低点时受到的力是( )
如图所示,细线的一端与一小球相连,另一端悬于固定点O,现使小球绕O点在竖直面内做圆周运动,当小球运动到最低点时受到的力是( )
 如图所示,细线的一端与一小球相连,另一端悬于固定点O,现使小球绕O点在竖直面内做圆周运动,当小球运动到最低点时受到的力是( )
如图所示,细线的一端与一小球相连,另一端悬于固定点O,现使小球绕O点在竖直面内做圆周运动,当小球运动到最低点时受到的力是( )| A. | 重力、拉力 | B. | 重力、向心力 | ||
| C. | 拉力、向心力 | D. | 重力、拉力、向心力 |
13. 如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )
如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )
 如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )
如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )| A. | t时刻B的速度大于A的速度 | |
| B. | t时刻B受到的合力等于零 | |
| C. | 0~t过程A的机械能增加量大于B的机械能减小量 | |
| D. | 0~t过程A的重力势能增加量大于B的重力势能减小量 |
10.下列说法中正确的是( )
| A. | 光的偏振现象说明光是横波 | |
| B. | 波的图象表示介质中“某个质点”在“各个时刻”的位移 | |
| C. | 均匀变化的磁场产生均匀变化的电场,均匀变化的电场产生变化的磁场 | |
| D. | 分别用红光和绿光在同一装置上进行双缝干涉实验,红光的干涉条纹间距较大 | |
| E. | 狭义相对论认为,在不同的惯性参考系中,一切物理规律都是相同的,真空中的光速也是相同的 |
11. 与一般吉他以箱体的振动发声不同,电吉他靠拾音器发声.如图所示,拾音器由小磁体及绕在其上的线圈组成.磁体产生的磁场使钢质琴弦磁化而产生磁性,即琴弦也产生自己的磁场.当某根琴弦被拨动而相对线圈振动时,线圈中就会产生相应的电流,并最终还原为声音信号.下列说法中正确的是( )
与一般吉他以箱体的振动发声不同,电吉他靠拾音器发声.如图所示,拾音器由小磁体及绕在其上的线圈组成.磁体产生的磁场使钢质琴弦磁化而产生磁性,即琴弦也产生自己的磁场.当某根琴弦被拨动而相对线圈振动时,线圈中就会产生相应的电流,并最终还原为声音信号.下列说法中正确的是( )
 与一般吉他以箱体的振动发声不同,电吉他靠拾音器发声.如图所示,拾音器由小磁体及绕在其上的线圈组成.磁体产生的磁场使钢质琴弦磁化而产生磁性,即琴弦也产生自己的磁场.当某根琴弦被拨动而相对线圈振动时,线圈中就会产生相应的电流,并最终还原为声音信号.下列说法中正确的是( )
与一般吉他以箱体的振动发声不同,电吉他靠拾音器发声.如图所示,拾音器由小磁体及绕在其上的线圈组成.磁体产生的磁场使钢质琴弦磁化而产生磁性,即琴弦也产生自己的磁场.当某根琴弦被拨动而相对线圈振动时,线圈中就会产生相应的电流,并最终还原为声音信号.下列说法中正确的是( )| A. | 换用尼龙材质的琴弦,电吉他仍能正常工作 | |
| B. | 若小磁体失去磁性,电吉他仍能正常工作 | |
| C. | 琴弦振动的过程中,线圈中电流的方向不会发生变化 | |
| D. | 拾音器的作用是利用电磁感应把琴弦的振动转化成电信号 |
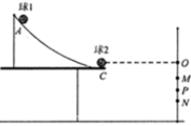 某同学用图示装置研究弹性正碰.实验中使用半径相等的弹性小球1和2,且小球1的质量大于小球2的质量.实验主要步骤如下:安装好实验装置,做好测量前的准备.
某同学用图示装置研究弹性正碰.实验中使用半径相等的弹性小球1和2,且小球1的质量大于小球2的质量.实验主要步骤如下:安装好实验装置,做好测量前的准备.