题目内容
16.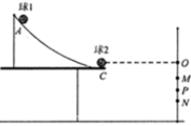 某同学用图示装置研究弹性正碰.实验中使用半径相等的弹性小球1和2,且小球1的质量大于小球2的质量.实验主要步骤如下:安装好实验装置,做好测量前的准备.
某同学用图示装置研究弹性正碰.实验中使用半径相等的弹性小球1和2,且小球1的质量大于小球2的质量.实验主要步骤如下:安装好实验装置,做好测量前的准备.第一步:先将木板竖直固定于斜槽前端边缘处的C点,且板面与纸面垂直,在木板上记下置于C点小球的位置O,然后将木板向右平移适当的距离,并固定.
第二步:不放小球2,让小球1从斜槽上A点由静止滚下,并撞在木板上,重复多次,用尽可能小的圆把小球的所有落点圈在里面,其圆心就是小球落点的平均位置.
第三步:把小球2放在斜槽前端边缘处的C点,让小球1从A点由静止滚下,使它们碰撞,重复多次,并使用与第二步同样的方法分别标出碰撞后两小球落点的平均位置.
第四步:用刻度尺分别测量三个落地点的平均位置到O点的距离,即线段OM、OP、ON的长度.
回答下列问题:
(1)若C点到木板的距离为x,小球落点到O点的距离为y,重力加速度为g,则小球做平抛运动的初速度v0=x$\sqrt{\frac{g}{2y}}$;
(2)上述实验中,P点是实验的第二步中小球1的的平均位置,N点是小球1与小球2碰撞后小球1落点的平均位置,M点是小球2落点的平均位置.
(3)若满足条件$\frac{1}{\sqrt{OP}}$=$\frac{1}{\sqrt{OM}}$-$\frac{1}{\sqrt{ON}}$(用测量量表示),则两小球发生的碰撞是弹性正碰.
分析 (1)通过平抛运动的知识,先根据高度求时间,再根据水平位移小球的初速度;
(2)根据题意:小球1的质量大于小球2的质量,第二步中两球碰撞后,球2的速度大,平抛运动的水平位移大,N点是其落点.碰后,球1的速度减小,将落在M点,可以得出三个点为小球的三个落地点的平均位置;
(3)根据动量守恒和机械能守恒列式,联立解得应满足的表达式.
解答 解:(1)根据平抛运动的规律可知,x=v0t
y=$\frac{1}{2}$gt2
联立解得:v0=x$\sqrt{\frac{g}{2y}}$
(2)由于三个小球飞行的水平距离相等,因此水平速度越大时,飞行时间越短;由于它们在竖直方向均做自由落体运动,故水平速度越大时,下落的高度越小;根据题意可知,小球1的质量大于小球2的质量,第二步中两球相碰后球1的速度减小,落在N点,球2的质量小,获得的速度大,落在M点,则第一步中球1落在中间位置P点,故P点是在实验的第一步中小球1落点的平均位置;N点是小球1与小球2碰撞后小球1落点的平均位置;M点是小球2落点的平均位置(3)如果满足动量守恒,则一定有:m1v0=m1v1+m2v2; (1)
如果为弹性碰撞,则有:$\frac{1}{2}$m1v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22 (2)
由平抛运动规律可知,v=x$\sqrt{\frac{g}{2y}}$,故v0=x$\sqrt{\frac{g}{2OP}}$;v1=x$\sqrt{\frac{g}{ON}}$;v2=x$\sqrt{\frac{g}{OM}}$
将求出的速度代入(1)、(2)两式;
联立解得:
$\frac{1}{\sqrt{OP}}$=$\frac{1}{\sqrt{OM}}$-$\frac{1}{\sqrt{ON}}$;
因此只有满足上式才能证明碰撞为弹性正碰;
故答案为:(1)x$\sqrt{\frac{g}{2y}}$;(2)实验的第二步中小球1的;小球1与小球2碰撞后小球1落点的;小球2落点;(3)$\frac{1}{\sqrt{OP}}$=$\frac{1}{\sqrt{OM}}$-$\frac{1}{\sqrt{ON}}$;
点评 本题考查动量守恒的验证实验,要注意明确实验原理,掌握平抛运动规律的应用,同时注意题目要求,本题中质量未知,是利用下落高度来确定是否为弹性碰撞的,不能利用质量关系表达式进行验证.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 简谐振动是往复的匀变速运动 | |
| B. | 匀速圆周运动是加速度不变的运动 | |
| C. | 当物体速度为零时,加速度一定为零 | |
| D. | 当物体做曲线运动时,所受的合外力不可能一直为零 |
 如图所示,在直线MN的上方区域中有匀强磁场,磁感应强度为B,一个带电粒子垂直于磁场从a点进入磁场,从b点离开磁场,已知带电粒子的电量为q,质量为m,从a点进入磁场的速度与MN的夹角为θ弧度,则( )
如图所示,在直线MN的上方区域中有匀强磁场,磁感应强度为B,一个带电粒子垂直于磁场从a点进入磁场,从b点离开磁场,已知带电粒子的电量为q,质量为m,从a点进入磁场的速度与MN的夹角为θ弧度,则( )| A. | 粒子带正电,它在磁场中运动的时间为$\frac{2mθ}{Bq}$ | |
| B. | 粒子带正电,它在磁场中运动的时间为$\frac{2m(π-θ)}{Bq}$ | |
| C. | 粒子带负电,它在磁场中运动的时间为$\frac{2mθ}{Bq}$ | |
| D. | 粒子带负电,它在磁场中运动的时间为$\frac{2m(π-θ)}{Bq}$ |
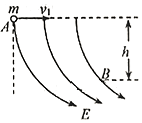 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,若A、B两点之间的高度差为h,则以下判断中正确的是( )| A. | A、B两点的电场强度和电势大小关系为EA<EB、φA>φB | |
| B. | 若带正电,则电场力一定做负功 | |
| C. | A、B两点间的电势差为$\frac{m}{2q}$(v22-v12-2gh) | |
| D. | 小球从A运动到B点的过程中电场力做的功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv2-mgh |
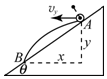 如图所示,从倾角为θ的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,以下说法正确的是( )
如图所示,从倾角为θ的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,以下说法正确的是( )| A. | 从抛出到落在斜面上B点所用时间为$\frac{{2{v_0}sinθ}}{g}$ | |
| B. | 从抛出到落在斜面上B点所用时间为$\frac{{2{v_0}tanθ}}{g}$ | |
| C. | 从抛出到离斜面最远时所用时间为$\frac{{{v_0}sinθ}}{g}$ | |
| D. | 从抛出到离斜面最远时所用时间为$\frac{{{v_0}tanθ}}{g}$ |
 搭载着航天员景海鹏、陈冬的神舟十一号载人飞船在酒泉卫星发射中心搭乘长征二号FY11火箭成功发射,在多次调整姿态后,于2016年10月19日3时31分顺利完成与天宫二号的对接任务,如图所示,已知天宫二号圆周轨道离地393公里,下列说法正确的是( )
搭载着航天员景海鹏、陈冬的神舟十一号载人飞船在酒泉卫星发射中心搭乘长征二号FY11火箭成功发射,在多次调整姿态后,于2016年10月19日3时31分顺利完成与天宫二号的对接任务,如图所示,已知天宫二号圆周轨道离地393公里,下列说法正确的是( )| A. | 飞船发射速度可能会超过11.2km/s | |
| B. | 飞船需要在较低的轨道上向后喷出炙热气体,才能完成与天宫二号的对接 | |
| C. | 飞船与天宫二号在同一轨道时向后喷出炙热气体,才能完成与天宫二号的对接 | |
| D. | 若已知飞船与天宫二号的“组合体”运行周期T、离地高度h、地球半径R,地球质量M,可求出“组合体”的质量 |
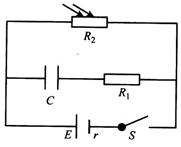 如图所示的电路中,R1是定值电阻,R2是光敏电阻,电源的内阻不能忽略.闭合开关S,当光敏电阻上的光照强度减弱时,下列说法正确的是( )
如图所示的电路中,R1是定值电阻,R2是光敏电阻,电源的内阻不能忽略.闭合开关S,当光敏电阻上的光照强度减弱时,下列说法正确的是( )| A. | 通过R2的电流增大 | B. | 电源的路端电压减小 | ||
| C. | 电容器C所带的电荷量增加 | D. | 电源的效率减小 |
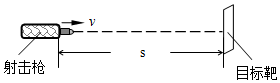
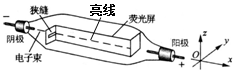 阴极射线管中电子束由阴极沿x轴正方向射出,在荧光屏上出现一条亮线(如图).要使该亮线向z轴正方向偏转,可加上沿( )
阴极射线管中电子束由阴极沿x轴正方向射出,在荧光屏上出现一条亮线(如图).要使该亮线向z轴正方向偏转,可加上沿( )| A. | z轴正方向的磁场 | B. | y轴负方向的磁场 | C. | z轴正方向的电场 | D. | y轴负方向的电场 |