题目内容
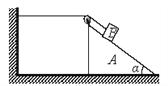
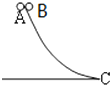
【题目】如图所示，足够长的传送带与水平面夹角为θ，以速度v0逆时针匀速转动．在传送带的上端轻轻放置一个质量为m的小木块，小木块与传送带间的动摩擦因数μ＜tanθ，则下图中能客观地反映小木块的速度随时间变化关系的是（ ）
A.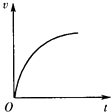
B.
C.
D.
【答案】D
【解析】解：初状态时：重力的分力与摩擦力均沿着斜面向下，且都是恒力，所以物体先沿斜面匀加速直线运动，
由牛顿第二定律得：
加速度：a1= 
=gsinθ+μgcosθ；
当小木块的速度与传送带速度相等时，由μ＜tanθ知道木块继续沿传送带加速向下，
但是此时摩擦力的方向沿斜面向上，再由牛顿第二定律求出此时的加速度：
a2= 
=gsinθ﹣μgcosθ；
比较知道a1＞a2，图象的斜率表示加速度，所以第二段的斜率变小．
故ABC不符合题意，D符合题意；
故答案为：D
本题需要分析出小木块的速度随时间的变化规律，则首先要分析小木块起始阶段的受力情况，因为皮带轮逆时针旋转，所以摩擦力是沿斜面向下，向下的力还有重力的下滑分力，并且它们都是恒力，所以小木块先沿斜面做匀加速直线运动，根据牛顿第二定律求出加速度，当小木块的速度与传送带的速度相等时，由μ＜tanθ知道木块继续沿传送带向下做加速运动，但此时的摩擦力沿斜面向上，再根据牛顿第二定律此处此时的加速度，再比较前后的加速度大小关系.
练习册系列答案
相关题目
