题目内容
18.早在19世纪.匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定会减轻”.后来,人们常把这类物理现象称之为“厄缶效应”.已知地球的半径R,考虑地球的自转,赤道处相对于地面静止的列车随地球自转的线速度为v0,列车的质量为m,此时列车对轨道的压力为N0.若列车相对地面正在以速率v沿水平轨道匀速向东行驶,此时列车对轨道的压力为N,那么,由于该火车向东行驶而引起列车对轨道的压力减轻的数量(N0一N)为是( )
| A. | m$\frac{{v}^{2}}{R}$ | B. | m$\frac{{v}_{0}v}{R}$ | C. | m$\frac{{v}^{2}+{v}_{0}v}{R}$ | D. | m$\frac{{v}^{2}+2{v}_{0}v}{R}$ |
分析 若仅仅考虑地球的自转影响时,火车绕地心做圆周运动的线速度大小为v0,根据牛顿运动定律求出火车对轨道的压力为N0;若这列火车相对地面又附加了一个线速度v,火车绕地心做圆周运动的线速度大小为v+v0,再由牛顿运动定律求出N,最后求出N0-N.
解答 解:若仅仅考虑地球的自转影响时,火车绕地心做圆周运动的线速度大小为 v0,以火车为研究对象,根据牛顿第二定律得:
mg-N0=m$\frac{{v}_{0}^{2}}{R}$,得到N0=mg-m$\frac{{v}_{0}^{2}}{R}$.
若这列火车相对地面又附加了一个线速度v,火车绕地心做圆周运动的线速度大小为v+v0,根据牛顿第二定律得:
mg-N=m$\frac{(v+{v}_{0})^{2}}{R}$,得到N′=mg-m$\frac{(v+{v}_{0})^{2}}{R}$
则N0-N=m$\frac{{v}^{2}+2{v}_{0}v}{R}$
故选:D.
点评 本题要建立模型,实际上就是一个竖直平面内圆周运动的类型.运用牛顿第二定律求解即可.

练习册系列答案
相关题目
8.在科学的发展历程中,许多科学家做出了杰出的贡献.下列叙述符合物理学史实的是( )
| A. | 开普勒以行星运动定律为基础总结出万有引力定律 | |
| B. | 卡文迪许通过实验测出了万有引力常量 | |
| C. | 牛顿提出了万有引力定律,并通过实验测出了万有引力常量 | |
| D. | 伽利略在前人的基础上通过观察总结得到行星运动三定律 |
9.“弹弹子”是我国传统的儿童游戏,如图所示,静置于水平地面的两个完全相同的弹子沿一直线排列,质量均为m,人在极短时间内给第一个弹子水平冲量I使其水平向右运动,当第一个弹子运动了距离L时与第二个弹子相碰,碰后第二个弹子运动了距离L时停止.已知摩擦阻力大小恒为弹子所受重力的k倍,重力加速度为g,若弹子之间碰撞时间极短,为弹性碰撞,忽略空气阻力,则人给第一个弹子水平冲量I为( )

| A. | m$\sqrt{6kgL}$ | B. | m$\sqrt{4kgL}$ | C. | m$\sqrt{2kgL}$ | D. | m$\sqrt{kgL}$ |
13. 如图所示,水平放置的圆盘绕中心轴勾OO′匀速转动,一物块P放在圆盘上并与圆盘相对静止,对物块受力分析正确的是,物块只受到( )
如图所示,水平放置的圆盘绕中心轴勾OO′匀速转动,一物块P放在圆盘上并与圆盘相对静止,对物块受力分析正确的是,物块只受到( )
 如图所示,水平放置的圆盘绕中心轴勾OO′匀速转动,一物块P放在圆盘上并与圆盘相对静止,对物块受力分析正确的是,物块只受到( )
如图所示,水平放置的圆盘绕中心轴勾OO′匀速转动,一物块P放在圆盘上并与圆盘相对静止,对物块受力分析正确的是,物块只受到( )| A. | 重力、弹力、摩擦力和向心力 | B. | 重力、弹力、摩擦力 | ||
| C. | 弹力、摩擦力 | D. | 重力、弹力 |
10. 示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )
示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )
 示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )
示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )| A. | 减小UXX | B. | 增大UXX | ||
| C. | 增大电子枪的加速电压 | D. | 减小电子枪的加速电压 |
7. 如图所示,在光滑水平地面上放着两个物体,其间用一根不能伸长的细绳相连,开始时B静止,A具有4kg•m/s的动量(以向右为正),刚开始绳松弛.在绳拉紧(可能拉断)的过程中,A、B动量的变化量可能为( )
如图所示,在光滑水平地面上放着两个物体,其间用一根不能伸长的细绳相连,开始时B静止,A具有4kg•m/s的动量(以向右为正),刚开始绳松弛.在绳拉紧(可能拉断)的过程中,A、B动量的变化量可能为( )
 如图所示,在光滑水平地面上放着两个物体,其间用一根不能伸长的细绳相连,开始时B静止,A具有4kg•m/s的动量(以向右为正),刚开始绳松弛.在绳拉紧(可能拉断)的过程中,A、B动量的变化量可能为( )
如图所示,在光滑水平地面上放着两个物体,其间用一根不能伸长的细绳相连,开始时B静止,A具有4kg•m/s的动量(以向右为正),刚开始绳松弛.在绳拉紧(可能拉断)的过程中,A、B动量的变化量可能为( )| A. | △PA=4kg•m/s,△PB=-4kg•m/s | B. | △PA=2kg•m/s,△PB=-2kg•m/s | ||
| C. | △PA=-2kg•m/s,△PB=2kg•m/s | D. | △PA=△PB=2kg•m/s |
 如图所示为测一块半球形玻璃砖的折射率的实验,实验的主要步骤如下:
如图所示为测一块半球形玻璃砖的折射率的实验,实验的主要步骤如下: 在地面附近竖直平面内有一范围足够大的互相正交的匀强电场和匀强磁场,磁感应强度大小为B,方向水平并垂直纸面向外,一个质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀强圆周运动,(重力加速度为g).求:
在地面附近竖直平面内有一范围足够大的互相正交的匀强电场和匀强磁场,磁感应强度大小为B,方向水平并垂直纸面向外,一个质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀强圆周运动,(重力加速度为g).求: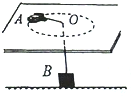 如图所示,高h=1.2m的水平桌面上有一光滑小孔O,长L=1.5m的细绳穿过小孔,一端与放在桌面上质量M=0.3kg的玩具汽车A相连,另一端竖直拉着质量m=0.1kg的物块B,当A在桌面上以速率v=1m/s绕小孔作匀速圆周运动时,绳被拉紧,物块B对地面的压力恰好为0,当A在桌面上以速率v=1.5m/s作匀速圆周运动时,B离地面的高度为0.375m.
如图所示,高h=1.2m的水平桌面上有一光滑小孔O,长L=1.5m的细绳穿过小孔,一端与放在桌面上质量M=0.3kg的玩具汽车A相连,另一端竖直拉着质量m=0.1kg的物块B,当A在桌面上以速率v=1m/s绕小孔作匀速圆周运动时,绳被拉紧,物块B对地面的压力恰好为0,当A在桌面上以速率v=1.5m/s作匀速圆周运动时,B离地面的高度为0.375m.