题目内容
8.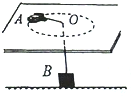 如图所示,高h=1.2m的水平桌面上有一光滑小孔O,长L=1.5m的细绳穿过小孔,一端与放在桌面上质量M=0.3kg的玩具汽车A相连,另一端竖直拉着质量m=0.1kg的物块B,当A在桌面上以速率v=1m/s绕小孔作匀速圆周运动时,绳被拉紧,物块B对地面的压力恰好为0,当A在桌面上以速率v=1.5m/s作匀速圆周运动时,B离地面的高度为0.375m.
如图所示,高h=1.2m的水平桌面上有一光滑小孔O,长L=1.5m的细绳穿过小孔,一端与放在桌面上质量M=0.3kg的玩具汽车A相连,另一端竖直拉着质量m=0.1kg的物块B,当A在桌面上以速率v=1m/s绕小孔作匀速圆周运动时,绳被拉紧,物块B对地面的压力恰好为0,当A在桌面上以速率v=1.5m/s作匀速圆周运动时,B离地面的高度为0.375m.
分析 当B对地面压力恰好为零时,绳子的拉力等于B的重力,结合牛顿第二定律求出A的速度.当速度为1.5m/s时,根据牛顿第二定律求出轨道半径,从而得出B离地的高度.
解答 解:当物块B对地面的压力恰好为零时,拉力F=mg=0.1×10N=1N,
根据$F=M\frac{{v}^{2}}{r}$得,$v=\sqrt{\frac{Fr}{M}}=\sqrt{\frac{1×(1.5-1.2)}{0.3}}m/s=1m/s$.
当 A的速度为1.5m/s时,F=mg,根据牛顿第二定律得,$F=M\frac{v{′}^{2}}{r′}$,
解得$r′=\frac{Mv{′}^{2}}{F}=\frac{0.3×1.{5}^{2}}{1}m=0.675m$,
则B离地的高度H=h-(L-r′)=1.2-(1.5-0.675)m=0.375m.
故答案为:1,0.375.
点评 解决本题的关键知道圆周运动向心力的来源,抓住拉力和B的重力相等,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
18.早在19世纪.匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定会减轻”.后来,人们常把这类物理现象称之为“厄缶效应”.
已知地球的半径R,考虑地球的自转,赤道处相对于地面静止的列车随地球自转的线速度为v0,列车的质量为m,此时列车对轨道的压力为N0.若列车相对地面正在以速率v沿水平轨道匀速向东行驶,此时列车对轨道的压力为N,那么,由于该火车向东行驶而引起列车对轨道的压力减轻的数量(N0一N)为是( )
已知地球的半径R,考虑地球的自转,赤道处相对于地面静止的列车随地球自转的线速度为v0,列车的质量为m,此时列车对轨道的压力为N0.若列车相对地面正在以速率v沿水平轨道匀速向东行驶,此时列车对轨道的压力为N,那么,由于该火车向东行驶而引起列车对轨道的压力减轻的数量(N0一N)为是( )
| A. | m$\frac{{v}^{2}}{R}$ | B. | m$\frac{{v}_{0}v}{R}$ | C. | m$\frac{{v}^{2}+{v}_{0}v}{R}$ | D. | m$\frac{{v}^{2}+2{v}_{0}v}{R}$ |
19.质量为2×103kg的汽车,以恒定功率60kw在水平公路上行驶,能达到的最大速度为30m/s,则当汽车的速度为15m/s时的加速度为( )
| A. | 0.5m/s2 | B. | 1m/s2 | C. | 1.5m/s2 | D. | 2m/s2 |
16.图示电路中,变压器为理想变压器,开关S闭合后,以下说法正确的是( )


| A. | 电表V1示数不变,V2示数减小 | B. | 电表A1、A2示数均增大 | ||
| C. | 电线圈输入功率减小 | D. | 电阻R1两端的电压减小 |
13.下列说法正确的是( )
| A. | 做功的力是矢量,所以功是矢量 | |
| B. | 力和位移都是矢量,所以功是矢量 | |
| C. | 功有正功和负功的区别,所以功是矢量 | |
| D. | 功是没有方向的,所以功是标量 |
18. 如图所示,当红蜡块从竖直放置的玻璃管的最下端开始匀速上升的同时,玻璃管水平向右匀速运动.红蜡块的运动轨迹为图中虚线甲,若要使红蜡块的运动轨迹沿图中虚线乙,则下列办法可行的是( )
如图所示,当红蜡块从竖直放置的玻璃管的最下端开始匀速上升的同时,玻璃管水平向右匀速运动.红蜡块的运动轨迹为图中虚线甲,若要使红蜡块的运动轨迹沿图中虚线乙,则下列办法可行的是( )
 如图所示,当红蜡块从竖直放置的玻璃管的最下端开始匀速上升的同时,玻璃管水平向右匀速运动.红蜡块的运动轨迹为图中虚线甲,若要使红蜡块的运动轨迹沿图中虚线乙,则下列办法可行的是( )
如图所示,当红蜡块从竖直放置的玻璃管的最下端开始匀速上升的同时,玻璃管水平向右匀速运动.红蜡块的运动轨迹为图中虚线甲,若要使红蜡块的运动轨迹沿图中虚线乙,则下列办法可行的是( )| A. | 增大玻璃管水平向右匀速运动的速度 | |
| B. | 减小玻璃管水平向右匀速运动的速度 | |
| C. | 使玻璃管的最下端沿虚线甲匀速运动 | |
| D. | 使玻璃管的最下端沿虚线乙匀速运动 |
 气压式保温瓶内密封空气体积为V,瓶内水面与出水口的高度差为h,如图所示,设水的密度为ρ,大气压强为p0,欲使水从出水口流出,瓶内空气的压强表达式为p0+ρgh,瓶内空气压缩量△V至少为$\frac{ρghV}{{p}_{0}+ρgh}$.
气压式保温瓶内密封空气体积为V,瓶内水面与出水口的高度差为h,如图所示,设水的密度为ρ,大气压强为p0,欲使水从出水口流出,瓶内空气的压强表达式为p0+ρgh,瓶内空气压缩量△V至少为$\frac{ρghV}{{p}_{0}+ρgh}$. 如图所示,O,A,B三点在同一水平直线上,O点有一个固定的水平长钉,A点为一固定点,OA相距L,B处有一小球,用一根长2L的轻绳和A点相连,现给B球一个竖直向下的速度v0.使它要能击中A点,求v0的最小值是多少?
如图所示,O,A,B三点在同一水平直线上,O点有一个固定的水平长钉,A点为一固定点,OA相距L,B处有一小球,用一根长2L的轻绳和A点相连,现给B球一个竖直向下的速度v0.使它要能击中A点,求v0的最小值是多少?