题目内容
14.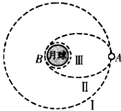 如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞船在圆形轨道I运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞船在圆形轨道I运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )| A. | 飞船在轨道Ⅱ上运行时通过B点的速度大于$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在轨道Ⅰ上的机械能大于在轨道Ⅱ上的机械能 | |
| C. | 飞船在轨道Ⅰ上运行时通过A点的加速度大于在轨道Ⅱ上运行时通过A点的加速度 | |
| D. | 飞船在轨道Ⅲ绕月球运行一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ |
分析 在月球表面,重力等于万有引力,在任意轨道,万有引力提供向心力,联立方程即可求解,
卫星变轨也就是近心运动或离心运动,根据提供的万有引力和所需的向心力关系确定.
飞船在近月轨道Ⅲ绕月球运行,重力提供向心力,根据向心力周期公式即可求解.
解答 解:A、飞船在轨道Ⅰ上,万有引力提供向心力:$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
在月球表面,万有引力等于重力得:$\frac{GMm}{{R}^{2}}$=mg0,
解得v=$\sqrt{{g}_{0}R}$,
在轨道Ⅰ上经过B点,在该位置加速,使万有引力小于向心力,做离心运动,才能进入轨道Ⅱ,所以在轨道Ⅰ上过B点时的速度小于轨道Ⅱ上过B点时的速度,
所以飞船在轨道Ⅱ上运行时通过B点的速度大于$\sqrt{{g}_{0}R}$,故A正确;
B、飞船在轨道Ⅰ上的机械能大于在轨道Ⅱ上的机械能,故B正确;
C、飞船在轨道Ⅰ上运行时通过A点和在轨道Ⅱ上运行时通过A点时受到的万有引力大小相等,根据牛顿第二定律可知加速度必定相等.故C错误.
D、设飞船在近月轨道Ⅲ绕月球运行一周所需的时间为T,则:
m$\frac{{4π}^{2}}{{T}^{2}}$R=mg0,
T=2π$\sqrt{\frac{R}{{g}_{0}}}$,故D正确.
故选:ABD.
点评 该题考查了万有引力公式及向心力基本公式的应用,难度不大,了解卫星如何变轨的理解,可以根据离心运动知识理解卫星变轨的问题..

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
4. 如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )
如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )
 如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )
如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )| A. | x可能是电感线圈,y可能是电容器 | B. | x可能是电容器,y可能是电感线圈 | ||
| C. | x可能是二极管,y可能是电容器 | D. | x可能是电感线圈,y可能是二极管 |
5.如图所示,当氢原子从n=4迁到n=2的能级和从n=3迁到n=1的能级时,分别辐射出光子a和光子b,则( )
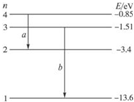

| A. | 由于放出光子,原子的能量增加 | |
| B. | 光子a的能量大于光子b的能量 | |
| C. | 光子a的波长大于光子b的波长 | |
| D. | 若光子a能使某金属发生光电效应,则光子b一定能使该金属发生光电效应 |
2.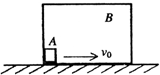 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )| A. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{6μg}$ | B. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{5μg}$ | ||
| C. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{7μg}$ | D. | t=$\frac{{5(\sqrt{v_0^2-2μgL}-\sqrt{2μgS})}}{7μg}$ |
6.如图所示,是一独立正点荷形成电场中的一条电场线,线段AB=BC,则( )


| A. | 电场强度比较是EA>EB | |
| B. | 电势比较是φA<φB | |
| C. | 电势差比较是UAB=UBC | |
| D. | 检验电荷沿AC方向移动电场力不做功 |
4.关于匀速圆周运动的角速度、线速度、周期和频率的说法,正确的是( )
| A. | 角速度与线速度成正比 | B. | 角速度与周期成反比 | ||
| C. | 线速度与周期成正比 | D. | 角速度与频率成反比 |