题目内容
3.一河宽为100m,水流速度3m/s,一小船横渡该河.已知小船在静水中的航速为5m/s.(1)若船头始终正对对岸航行,问小船经过多长时间到达对岸?
(2)若要使小船沿垂直于河岸的方向航行,则船头的方向如何?渡河所经历的时间是多少?
分析 (1)将小船运动分解为沿河岸方向和垂直于河岸方向,根据垂直于河岸方向上的速度求出渡河的时间.
(2)当合速度与河岸垂直时,将运行到正对岸,求出合速度的大小,根据河岸求出渡河的时间.
解答 解:(1)因船头始终正对对岸航行,则渡河时间t=$\frac{d}{{v}_{c}}$=$\frac{100}{5}$s=20s.
(2)当合速度与河岸垂直,小船到达正对岸.设静水速的方向与河岸的夹角为θ.
cosθ=$\frac{{v}_{s}}{{v}_{c}}$=$\frac{3}{5}$,知θ=53°.
合速度的大小为v=$\sqrt{{v}_{c}^{2}-{v}_{s}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4m/s
则渡河时间t′=$\frac{d}{v}$=$\frac{100}{4}$s=25s.
答:(1)当船头始终正对着对岸时,小船经过20s时间到达对岸;
(2)如果小船的路径要与河岸垂直,应偏上游夹角为53°,消耗的时间是25s.
点评 解决本题的关键知道分运动与合运动具有等时性,以及各分运动具有独立性,互不干扰.

练习册系列答案
相关题目
13.关于磁感强度,下列说法正确的是( )
| A. | 磁感强度表示磁场的强弱 | |
| B. | 磁感线密的地方,磁感强度大 | |
| C. | 空间某点的磁感强度的方向就是该点的磁场方向 | |
| D. | 磁感强度的方向就是通电导线在磁场中的受力方向 |
14.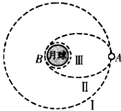 如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞船在圆形轨道I运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞船在圆形轨道I运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
 如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞船在圆形轨道I运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞船在圆形轨道I运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )| A. | 飞船在轨道Ⅱ上运行时通过B点的速度大于$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在轨道Ⅰ上的机械能大于在轨道Ⅱ上的机械能 | |
| C. | 飞船在轨道Ⅰ上运行时通过A点的加速度大于在轨道Ⅱ上运行时通过A点的加速度 | |
| D. | 飞船在轨道Ⅲ绕月球运行一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ |
11.如图所示为LC振荡电路中电容器的极板带电荷量随时间变化曲线,下列判断中正确的是( )
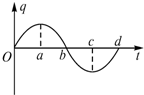

| A. | 在b和d时刻,电路中电流最小 | B. | 在a→b时间内,电场能转变为磁场能 | ||
| C. | a和c时刻,电场能能为零 | D. | 在O→a和c→d时间内,电容器被充电 |
18.物体受到一组共点恒力作用而处于平衡状态,当撤去其中某个恒力时,物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | C. | 匀变速曲线运动 | D. | 变加速曲线运动 |
12.关于物体的动量,下列说法正确的是( )
| A. | 物体的动量越大,它的惯性也越大 | |
| B. | 动量是矢量,其方向一定与物体速度的方向相同 | |
| C. | 动量大的物体,它的速度可能大 | |
| D. | 物体的动量越大,它所受的合外力越大 |
13.对于向心加速度的公式a=ω2r,a=$\frac{{v}^{2}}{r}$的说法正确的是( )
| A. | a与r成正比 | B. | a与r成反比 | ||
| C. | 在r不变时,a与ω成正比 | D. | 在r不变时,a与υ2成正比 |
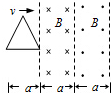 如图所示,一边长为a,电阻为R的等边三角形线框在外力作用下以速度v匀速穿过宽度均为a的两个匀强磁场区域,两磁场磁感应强度的大小均为B,方向相反,线框运动方向与底边平行且与磁场边缘垂直.以逆时针方向为电流正方向,从图示位置开始线框中感应电流I与沿运动方向的位移x的关系图象为( )
如图所示,一边长为a,电阻为R的等边三角形线框在外力作用下以速度v匀速穿过宽度均为a的两个匀强磁场区域,两磁场磁感应强度的大小均为B,方向相反,线框运动方向与底边平行且与磁场边缘垂直.以逆时针方向为电流正方向,从图示位置开始线框中感应电流I与沿运动方向的位移x的关系图象为( )



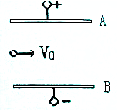 质量m=0.1kg,带电荷量q=-4×10-7C的带电微粒以v0=10m/s的速度从水平放置的平行金属板A、B的中央飞入板间,如图所示,已知板长L=1.0m,板间距离d=0.06m,问AB间所加电压在什么范围内带电粒子能从板间飞出?
质量m=0.1kg,带电荷量q=-4×10-7C的带电微粒以v0=10m/s的速度从水平放置的平行金属板A、B的中央飞入板间,如图所示,已知板长L=1.0m,板间距离d=0.06m,问AB间所加电压在什么范围内带电粒子能从板间飞出?