题目内容
16.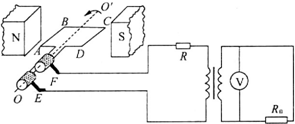 如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )| A. | 变压器原线圈两端的电压为100V | |
| B. | 电阻R的功率为10W | |
| C. | 电动势的有效值为110V | |
| D. | 电动势瞬时值表达式为e=112$\sqrt{2}$cosπtV |
分析 由变压器的匝数与电压关系判定原线圈两端的电压;由欧姆定律求出副线圈中的电流,然后再根据电流与匝数的关系求出原线圈中的电流,由P=I2R求出R中的电功率;由U=IR求出R两端的电压,然后求出电源的电动势;由交流电的产生的原理求出电动势表达式.
解答 解:A、降压变压器原副线圈匝数比为10:1,电压表的示数为10V,则:$\frac{{U}_{1}}{{U}_{2}}=\frac{{n}_{1}}{{n}_{2}}$,所以:${U}_{1}=\frac{{n}_{1}}{{n}_{2}}•{U}_{2}=\frac{10}{1}×10=100$V.故A正确;
B、副线圈中的电流:${I}_{2}=\frac{{U}_{2}}{{R}_{0}}=\frac{10}{10}=1$A,根据:$\frac{{I}_{1}}{{I}_{2}}=\frac{{n}_{2}}{{n}_{1}}$,所以:${I}_{1}=\frac{{n}_{2}}{{n}_{1}}•{I}_{1}=\frac{1}{10}×1=0.1$A,电阻R的功率为${P}_{1}={I}_{1}^{2}R=0.{1}^{2}×100=1$W.故B错误;
C、电阻R两端的电压:UR=I1R=0.1×100=10V,电源产生的电动势:E=U1+UR+I1r=100+10+0.1×20=112V.故C错误;
D、线圈转速为50r/s,则:ω=2nπ=2π×50=100π,由于是从与中性面的位置开始计时,所以电动势瞬时值表达式为e=112$\sqrt{2}$cos100πtV.故D正确.
故选:AD
点评 本题考查交变电流的产生及有效值的定义,要注意明确电流表示数、机器铭牌上所标的电流值、电压值等均为有效值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 传送带是应用广泛的一种传动装置.在一水平向右匀速运动的传送带的左端A点,每隔相同的时间T,轻放上一个相同的工件.已知工件与传送带间动摩擦因数为μ,工件质量为m.经测量,发现前面那些已经和传送带达到相同速度的工件之间的距离均为L.已知重力加速度为g,下列判断正确的有( )
传送带是应用广泛的一种传动装置.在一水平向右匀速运动的传送带的左端A点,每隔相同的时间T,轻放上一个相同的工件.已知工件与传送带间动摩擦因数为μ,工件质量为m.经测量,发现前面那些已经和传送带达到相同速度的工件之间的距离均为L.已知重力加速度为g,下列判断正确的有( )
 传送带是应用广泛的一种传动装置.在一水平向右匀速运动的传送带的左端A点,每隔相同的时间T,轻放上一个相同的工件.已知工件与传送带间动摩擦因数为μ,工件质量为m.经测量,发现前面那些已经和传送带达到相同速度的工件之间的距离均为L.已知重力加速度为g,下列判断正确的有( )
传送带是应用广泛的一种传动装置.在一水平向右匀速运动的传送带的左端A点,每隔相同的时间T,轻放上一个相同的工件.已知工件与传送带间动摩擦因数为μ,工件质量为m.经测量,发现前面那些已经和传送带达到相同速度的工件之间的距离均为L.已知重力加速度为g,下列判断正确的有( )| A. | 传送带的速度大小为$\frac{L}{T}$ | |
| B. | 工件在传送带上加速时间为$\frac{L}{2μgT}$ | |
| C. | 每个工件与传送带间因摩擦而产生的热量为$\frac{μmgL}{2}$ | |
| D. | 传送带因传送每一个工件而多消耗的能量为$\frac{{m{L^2}}}{T^2}$ |
1.下面关于摩擦力做功的叙述中,正确的是( )
| A. | 静摩擦力对物体一定不做功 | |
| B. | 滑动摩擦力对物体一定做负功 | |
| C. | 一对静摩擦力中,一个做正功,另一个一定做负功 | |
| D. | 一对滑动摩擦力中,一个做负功,另一个一定做正功 |
8.站在高跳台上的跳水运动员,向上跳起后翻腾三周半竖直地插入水中,则从运动员刚起跳后到手指刚触及水面的这一过程中(忽略空气阻力,可以把人视为质点)( )
| A. | 运动员的机械能增加 | B. | 运动员的机械能减少 | ||
| C. | 运动员的势能不断增加 | D. | 运动员减少的重力势能转化为动能 |
 如图所示,一列简谐横波在t=0时刻的波的图象,A、B、C是介质中的三个质点.已知波是向x正方向传播的,波速为v=20m/s.请回答下列问题:
如图所示,一列简谐横波在t=0时刻的波的图象,A、B、C是介质中的三个质点.已知波是向x正方向传播的,波速为v=20m/s.请回答下列问题: 某研究小组的同学设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直浸入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针M,使M正好挡住P1、P2,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据M所插的位置,就可直接读出液体折射率的值,则:
某研究小组的同学设计了一个测量液体折射率的仪器,如图所示.在一圆盘上,过其圆心O作两条互相垂直的直径BC、EF,在半径OA上,垂直盘面插下两枚大头针P1、P2并保持P1、P2位置不变,每次测量时让圆盘的下半部分竖直浸入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针M,使M正好挡住P1、P2,同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据M所插的位置,就可直接读出液体折射率的值,则: 有一弹簧振子在水平方向上的BC之间做简谐运动,已知BC间的距离为20cm,振子在2s内完成了10次全振动.若从某时刻振子经过平衡位置时开始计时(t=0),经过$\frac{1}{4}$周期振子有正向最大加速度.
有一弹簧振子在水平方向上的BC之间做简谐运动,已知BC间的距离为20cm,振子在2s内完成了10次全振动.若从某时刻振子经过平衡位置时开始计时(t=0),经过$\frac{1}{4}$周期振子有正向最大加速度. 在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图所示,用米尺测量金属丝的长度l=1.010m.金属丝的电阻大约为4Ω.先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该金属材料的电阻率.
在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图所示,用米尺测量金属丝的长度l=1.010m.金属丝的电阻大约为4Ω.先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该金属材料的电阻率. 如图所示,是一个透明圆柱体的横截面,其半径为R,折射率是$\sqrt{3}$,AB是一条直线,今有一束平行光沿着AB方向射向圆柱体,若一条入射光线经折射后恰好经过B点.
如图所示,是一个透明圆柱体的横截面,其半径为R,折射率是$\sqrt{3}$,AB是一条直线,今有一束平行光沿着AB方向射向圆柱体,若一条入射光线经折射后恰好经过B点.