题目内容
11. 有一弹簧振子在水平方向上的BC之间做简谐运动,已知BC间的距离为20cm,振子在2s内完成了10次全振动.若从某时刻振子经过平衡位置时开始计时(t=0),经过$\frac{1}{4}$周期振子有正向最大加速度.
有一弹簧振子在水平方向上的BC之间做简谐运动,已知BC间的距离为20cm,振子在2s内完成了10次全振动.若从某时刻振子经过平衡位置时开始计时(t=0),经过$\frac{1}{4}$周期振子有正向最大加速度.(1)求振子的振幅和周期;
(2)在图中作出该振子的位移-时间图象;
(3)写出振子的振动表达式.
分析 (1)振幅是振子离开平衡位置的最大距离,B、C间的距离等于2A.振子完成一次全振动所用的时间即为一个周期.
(2)由振子经过平衡位置时开始计时,振动方程是正弦函数.经过$\frac{1}{4}$周期,振子具有正向最大加速度,位移为负向最大.即可写出振子的振动方程.根据数学知识作出振子的位移-时间图象.
(3)根据y-t图象写出振动方程即可.
解答 解:(1)振子的振幅为:A=10cm
振子的周期为T=0.2s
(2)振子的位移--时间图象如图所示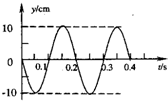
(3)$ω=\frac{2π}{T}=10πrad/s$
振子的振动方程为y=-Asinωt=-10sin 10πt.
答:(1)振子的振幅为10cm,周期为0.2s;
(2)该振子的位移--时间图象如图所示;
(3)振子的振动方程为y=-10sin 10πt.
点评 本题要理解并掌握振幅和周期的概念,要能根据t=0时刻的状态写出振动方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.一弹簧振子,使其离开平衡位置2cm,由静止开始释放,若t=0.1s时,第一次回到平衡位置,则下列说法中错误的是( )
| A. | 振子的振动周期为0.4s | |
| B. | 1s内振子通过的路程是20cm | |
| C. | t1=0.05s与t2=0.15s时刻,振子速度相同,加速度相同 | |
| D. | t1=0.05s与t2=0.35s时刻,振子速度方向相反,弹簧长度相等 |
2. 如图所示,长为L的轻杆一端固定质量为m的小球,另一端固定在转轴O上,现使小球在竖直平面内做圆周运动,p为圆周的最高点,若小球通过圆轨道最低点时速度大小为$\sqrt{\frac{9gL}{2}}$,忽略摩擦阻力和空气阻力,则下列判断正确的是( )
如图所示,长为L的轻杆一端固定质量为m的小球,另一端固定在转轴O上,现使小球在竖直平面内做圆周运动,p为圆周的最高点,若小球通过圆轨道最低点时速度大小为$\sqrt{\frac{9gL}{2}}$,忽略摩擦阻力和空气阻力,则下列判断正确的是( )
 如图所示,长为L的轻杆一端固定质量为m的小球,另一端固定在转轴O上,现使小球在竖直平面内做圆周运动,p为圆周的最高点,若小球通过圆轨道最低点时速度大小为$\sqrt{\frac{9gL}{2}}$,忽略摩擦阻力和空气阻力,则下列判断正确的是( )
如图所示,长为L的轻杆一端固定质量为m的小球,另一端固定在转轴O上,现使小球在竖直平面内做圆周运动,p为圆周的最高点,若小球通过圆轨道最低点时速度大小为$\sqrt{\frac{9gL}{2}}$,忽略摩擦阻力和空气阻力,则下列判断正确的是( )| A. | 小球不能到达p点 | |
| B. | 小球到达p点时的速度小于$\sqrt{gL}$ | |
| C. | 小球能到达p点,且在p点受到轻杆向上的弹力 | |
| D. | 小球能到达p点,且在p点受到轻杆向下的弹力 |
19.关于简谐振动回复力的说法正确的是( )
| A. | 回复力F=-kx中的x是指振子相对平衡位置的位移 | |
| B. | 回复力F=-kx中的x是指振子初位置指向末位置的位移 | |
| C. | 振子的回复力一定是合外力 | |
| D. | 振子的回复力不一定是合外力 |
16.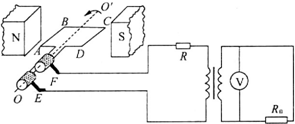 如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
 如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )| A. | 变压器原线圈两端的电压为100V | |
| B. | 电阻R的功率为10W | |
| C. | 电动势的有效值为110V | |
| D. | 电动势瞬时值表达式为e=112$\sqrt{2}$cosπtV |
3.关于第一宇宙速度,下列说法中正确的是( )
| A. | 它是人造地球卫星绕地球飞行的最小速度 | |
| B. | 它是近地圆形轨道上人造地球卫星的运行速度 | |
| C. | 它是能使卫星进入地球圆形轨道的最大发射速度 | |
| D. | 它是对应的轨道是椭圆 |
20.在不考虑空气阻力的情况下,下列物体中做平抛运动的是( )
| A. | 水平射出的子弹 | B. | 水平击出的排球 | ||
| C. | 斜向上踢出的足球 | D. | 从桌面上弹起的乒乓球 |
 两列波源振动情况完全相同的相干波在同一水平面上传播,两列波的振幅均为A,某时刻它们的波峰、波谷位置如图所示.回答下列问题:
两列波源振动情况完全相同的相干波在同一水平面上传播,两列波的振幅均为A,某时刻它们的波峰、波谷位置如图所示.回答下列问题: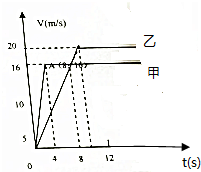 甲、乙两物体同时、同地、同向由静止出发,甲做匀加速直线运动,加速度为4米/秒2,4秒后改为匀速直线运动,乙做匀加速直线运动,加速度为2米/秒2,10秒后改为匀速直线运动,求乙追上甲之前他们之间的最大距离.
甲、乙两物体同时、同地、同向由静止出发,甲做匀加速直线运动,加速度为4米/秒2,4秒后改为匀速直线运动,乙做匀加速直线运动,加速度为2米/秒2,10秒后改为匀速直线运动,求乙追上甲之前他们之间的最大距离.