题目内容
6. 如图所示,是一个透明圆柱体的横截面,其半径为R,折射率是$\sqrt{3}$,AB是一条直线,今有一束平行光沿着AB方向射向圆柱体,若一条入射光线经折射后恰好经过B点.
如图所示,是一个透明圆柱体的横截面,其半径为R,折射率是$\sqrt{3}$,AB是一条直线,今有一束平行光沿着AB方向射向圆柱体,若一条入射光线经折射后恰好经过B点.(1)画出经过B点的光线及从圆柱体射出后的传播路径;
(2)经过B点的入射光线在圆柱体中的长度是多少?
分析 (1)画出光路图,由折射定律得到入射角与折射角的关系.再画出光路图.
(2)由几何关系也得到入射角与折射角的关系,即可求出入射角与折射角,再根据几何知识求解即可.
解答  解:(1)根据几何关系和光路可逆性,画出光路如图所示.
解:(1)根据几何关系和光路可逆性,画出光路如图所示.
(2)设光线P经C折射后过B点,根据折射定律有:
n=$\frac{sinα}{sinβ}$=$\sqrt{3}$…①
在△OBC中,由几何关系得:α=2β…②
由①、②得:2cosβ=$\sqrt{3}$…③
可得:β=30°,α=60°…④
所以 CB=2Rcosβ=$\sqrt{3}$R…⑤
答:
(1)画出经过B点的光线及从圆柱体射出后的传播路径如图;
(2)经过B点的入射光线在圆柱体中的长度是$\sqrt{3}$R.
点评 对于几何光学问题,首先要正确作出光路图,其次要充分运用几何知识分析入射角与折射角的关系,再根据折射定律进行解题.

练习册系列答案
相关题目
16.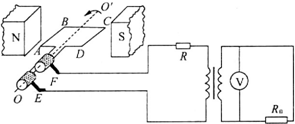 如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
 如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )| A. | 变压器原线圈两端的电压为100V | |
| B. | 电阻R的功率为10W | |
| C. | 电动势的有效值为110V | |
| D. | 电动势瞬时值表达式为e=112$\sqrt{2}$cosπtV |
17. 如图所示的空间存在匀强电场E,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf为水平面且与电场方向平行,bedf平面与电场垂直.下列说法中正确的是( )
如图所示的空间存在匀强电场E,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf为水平面且与电场方向平行,bedf平面与电场垂直.下列说法中正确的是( )
 如图所示的空间存在匀强电场E,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf为水平面且与电场方向平行,bedf平面与电场垂直.下列说法中正确的是( )
如图所示的空间存在匀强电场E,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心的球面上的点,aecf为水平面且与电场方向平行,bedf平面与电场垂直.下列说法中正确的是( )| A. | 将一个点电荷+q在球面上任意两点间移动时,电场力一定做功 | |
| B. | 将一个点电荷+q在球面上移动,从a 点移到c点的过程中,其电势能增加最多 | |
| C. | a点的电势和场强大于f点的电势和场强 | |
| D. | b、d两点的电势相同,电场强度不相同 |
14.如图甲、乙分别表示两种电压的波形,其中图甲所示电压按正弦规律变化.下列说法正确的是( )


| A. | 图甲表示交流电,图乙表示直流电 | |
| B. | 两种电压的周期相等 | |
| C. | 两种电压的有效值相等 | |
| D. | 图甲所示电压的瞬时值表达式为u=311sin100πtV |
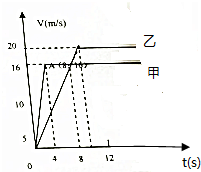 甲、乙两物体同时、同地、同向由静止出发,甲做匀加速直线运动,加速度为4米/秒2,4秒后改为匀速直线运动,乙做匀加速直线运动,加速度为2米/秒2,10秒后改为匀速直线运动,求乙追上甲之前他们之间的最大距离.
甲、乙两物体同时、同地、同向由静止出发,甲做匀加速直线运动,加速度为4米/秒2,4秒后改为匀速直线运动,乙做匀加速直线运动,加速度为2米/秒2,10秒后改为匀速直线运动,求乙追上甲之前他们之间的最大距离. 如图1所示,一小物体自A点获得某一初速度后开始沿水平面向左运动,然后沿斜面上滑,小物体从离开A点开始其速率随时间变化的图象如图2所示.已知物体与水平面和斜面间的动摩擦因数相同,取g=10m/s2.求:
如图1所示,一小物体自A点获得某一初速度后开始沿水平面向左运动,然后沿斜面上滑,小物体从离开A点开始其速率随时间变化的图象如图2所示.已知物体与水平面和斜面间的动摩擦因数相同,取g=10m/s2.求: 如图所示,在一固定光滑的竖直圆轨道,A、B两点分别是轨道的最高点和最低点,在其内轨道上有一质量为m的光滑小球能绕轨道做圆周运动,求:
如图所示,在一固定光滑的竖直圆轨道,A、B两点分别是轨道的最高点和最低点,在其内轨道上有一质量为m的光滑小球能绕轨道做圆周运动,求:
