Question

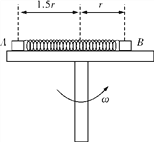
【题目】如图所示，叠放在水平转台上的物体 A，B，C 能随转台一起以角速度ω 匀速转 动，A，B，C 的质量分别为 3m、2m、m，A 与 B，B 和 C 与转台间的动摩擦因数都为 μ，A 和 B，C 离转台中心的距离分别为 r、1.5r． 设最大静摩擦力等于滑动摩擦力，下列说法正确的是（ ）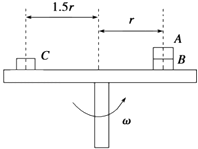

A.B 对 A 的摩擦力一定为 3μmg
B.B 对 A 的摩擦力一定为 3mω2r
C.转台的角速度一定满足ω≤
D.转台的角速度一定满足ω≤

Answer 1

【答案】B,D
【解析】解：A、对A受力分析，受重力、支持力以及B对A的静摩擦力，静摩擦力提供向心力，有f=（3m）ω2r≤μ（3m）g．故A错误，B正确．

C、由于A、AB整体、C受到的静摩擦力均提供向心力，故

对A，有：（3m）ω2r≤μ（3m）g

对AB整体，有：（3m+2m）ω2r≤μ（3m+2m）g

对物体C，有：mω2（1.5r）≤μmg

解得 ，故C错误，D正确．

故选：BD

【考点精析】根据题目的已知条件，利用匀速圆周运动和向心力的相关知识可以得到问题的答案，需要掌握匀速圆周运动线速度的大小恒定，角速度、周期和频率都是恒定不变的，向心加速度和向心力的大小也都是恒定不变的，是速度大小不变而速度方向时刻在变的变速曲线运动；向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力．