题目内容
8.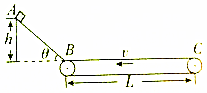 如图所示,AB是高h=0.75m,倾角θ=37°的粗糙斜面,斜面底端通过一小段圆弧与长L=4m的水平传送带左端相切,现将一小滑块从斜面顶端A由静止释放,已知滑块与斜面间的动摩擦因数μ1=0.3,滑块与传送带间的动摩擦因数μ2=0.2,不计空气阻力.取g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,AB是高h=0.75m,倾角θ=37°的粗糙斜面,斜面底端通过一小段圆弧与长L=4m的水平传送带左端相切,现将一小滑块从斜面顶端A由静止释放,已知滑块与斜面间的动摩擦因数μ1=0.3,滑块与传送带间的动摩擦因数μ2=0.2,不计空气阻力.取g=10m/s2,sin37°=0.6,cos37°=0.8.(1)求滑块经过B点时的速度;
(2)若传送带以v=3m/s的速度沿逆时针方向转动,试判断滑块能否向右滑离出传送带?若能,试求出滑离速度;若不能,则求出滑块第一次在传送带上做往返运动的时间.
分析 (1)根据牛顿第二定律求出滑块在斜面上的加速度,结合速度位移公式求出在B点的速度.
(2)根据牛顿第二定律求出滑块在传送带上的加速度大小,根据速度位移公式求出在传送带上匀减速直线运动的位移,判断是否从传送带右端滑出,若未滑出,返回做匀加速直线运动,结合运动学公式分析判断.
解答 解:(1)根据牛顿第二定律得,滑块在斜面上的加速度大小为:
${a}_{1}=\frac{mgsin37°-{μ}_{1}mgcos37°}{m}$=gsin37°-μ1gcos37°=6-0.3×8=3.6m/s2,
根据速度位移公式得:
${v}_{B}=\sqrt{2{a}_{1}•\frac{h}{sin37°}}$=$\sqrt{2×3.6×\frac{0.75}{0.6}}m/s=3m/s$.
(2)滑块在传送带上运动的加速度大小为:${a}_{2}={μ}_{2}g=2m/{s}^{2}$,
则匀减速运动的位移大小为:${x}_{1}=\frac{{{v}_{B}}^{2}}{2{a}_{2}}=\frac{9}{4}m=2.25m<4m$,可知滑块不能向右滑出传送带.
因为滑块滑上传送带的速度大小与传送带的速度大小相等,可知滑块先做匀减速直线运动,然后做匀加速直线运动,返回到B点,速度恰好达到传送带速度,大小为3m/s.
则往返的运动时间为:t=$2×\frac{v}{{a}_{2}}=2×\frac{3}{2}s=3s$.
答:(1)滑块经过B点的速度大小为3m/s;
(2)滑块滑离的速度为3m/s,在传送带上的往返时间为3s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,理清滑块在整个过程中的运动规律是解决本题的关键,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.把太阳系各行星的运动近似看做匀速圆周运动,则离太阳越远的行星( )
| A. | 周期越小 | B. | 线速度越大 | C. | 角速度越小 | D. | 加速度越大 |
16.由于某种原因,人造地球卫星的轨道半径减小了,那么,卫星的( )
| A. | 速率变小,周期变大 | B. | 速率变大,周期变大 | ||
| C. | 速率变大,周期变小 | D. | 速率变小,周期变小 |
13.如图甲,质量相等的a、b两物体,从斜面上的同一位置A由静止下滑,经B点在水平面上滑行一段时间后停下.不计经过B点时的能量损失,用传感器采集到它们的速度一时间图象如图图乙,则下列说法正确的是( )


| A. | a在水平面上滑行的距离比b的长 | |
| B. | a与斜面间的动摩擦因数比b的大 | |
| C. | 在整个运动过程中a,b两物体滑行的距离可能相等 | |
| D. | a在整个运动过程中克服摩擦力做的功比b的多 |
20. 如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )
如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )
 如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )
如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )| A. | 月球的质量 | B. | 地球的质量 | ||
| C. | “嫦娥一号”卫星的质量 | D. | 月球对“嫦娥一号”卫星的引力 |
15.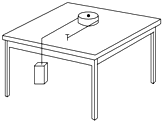 质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )
 质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )| A. | $\frac{mg}{2M}$ | B. | $\frac{mg}{M+m}$ | C. | $\frac{2mg}{M+4m}$ | D. | $\frac{2mg}{M+2m}$ |
16.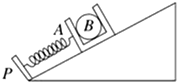 如图所示,置于足够长斜劈上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜劈上表面光滑静置于粗糙水平地面上.一轻质弹簧的一端与固定在斜劈上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜劈始终相对于地面处于静止状态( )
如图所示,置于足够长斜劈上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜劈上表面光滑静置于粗糙水平地面上.一轻质弹簧的一端与固定在斜劈上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜劈始终相对于地面处于静止状态( )
 如图所示,置于足够长斜劈上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜劈上表面光滑静置于粗糙水平地面上.一轻质弹簧的一端与固定在斜劈上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜劈始终相对于地面处于静止状态( )
如图所示,置于足够长斜劈上的盒子A内放有光滑球B,B恰与盒子前、后壁接触,斜劈上表面光滑静置于粗糙水平地面上.一轻质弹簧的一端与固定在斜劈上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放盒子,释放盒子前后斜劈始终相对于地面处于静止状态( )| A. | 弹簧恢复原长时AB速度最大 | |
| B. | 弹簧恢复原长时B对A的作用力为0 | |
| C. | AB沿斜面向上运动的过程中地面对斜劈的支持力不断变小 | |
| D. | AB沿斜面向上运动的过程中地面对斜劈的摩擦力始终向左 |