题目内容
【题目】如图所示，光滑杆O′A的O′端固定一根劲度系数为k=10N/m，原长为l0=1m的轻弹簧，质量为m=1kg的小球套在光滑杆上并与弹簧的上端连接，OO′为过O点的竖直轴，杆与水平面间的夹角始终为θ=30°，开始杆是静止的，当杆以OO′为轴转动时，角速度从零开始缓慢增加，直至弹簧伸长量为0.5m，下列说法正确的是（ ）
A.杆保持静止状态，弹簧的长度为0.5m
B.当弹簧伸长量为0.5m时，杆转动的角速度为 
rad/s
C.当弹簧恢复原长时，杆转动的角速度为 
rad/s
D.在此过程中，杆对小球做功为12.5J
【答案】A,B,D
【解析】解：A、当杆静止时，小球受力平衡，根据力的平衡条件可得：mgsin30°=kx，代入数据解得：x=0.5m，所以弹簧的长度为：l1=l0﹣x=0.5m，故A正确；
B、当弹簧伸长量为0.5m时，小球受力如图示：
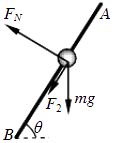
水平方向上：F2cos30°+Nsin30°=mω22（l0+x）cos30°
竖直方向上：Ncos30°=mg+F2sin30°
弹簧的弹力为：F2=kx
联立解得：ω2= 
rad/s，故B正确；
C、当弹簧恢复原长时，由牛顿第二定律可得：mgtan30°=mω12l0cos30°，解得：ω1= 
rad/s，故C错误；
D、在此过程中，由动能定理可得：W﹣mg2xsin30°= 
m[ω2（l0+x）cos30°]2﹣0，解得：W=12.5J，故D正确．
故选：ABD．
【考点精析】通过灵活运用动能定理的综合应用，掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷即可以解答此题．
