题目内容
1. 如图,战机在斜坡上方进行投弹演练,斜坡上a、b、c、d共线,且ab=bc=cd,战机水平匀速飞行,每隔相等时间释放一颗炸弹,第一颗落在a点,第三颗落在d点.不计空气阻力,第二颗炸弹可能落在( )
如图,战机在斜坡上方进行投弹演练,斜坡上a、b、c、d共线,且ab=bc=cd,战机水平匀速飞行,每隔相等时间释放一颗炸弹,第一颗落在a点,第三颗落在d点.不计空气阻力,第二颗炸弹可能落在( )| A. | ab之间 | B. | b点 | C. | c点 | D. | cd之间 |
分析 飞机与炮弹的水平速度相同,则落点在飞机的正下方,据水平向与竖直向的位移关系画图分析,从而再确定落点.
解答 解:如图作出过a点的水平直线,设第三颗炸弹该直线的D点,第二颗经过BQ点; 设炸弹经过aD面时的速度为vy;
取ad的中点O过竖直线OO′;
设aB=BD=x0,ab=bc=cd=L;
对第三颗炸弹有:水平方向上,x3=3Lcosθ-2x0=v0t1
竖直方向上有:y3=Ⅰ+$\frac{1}{2}$gt12
对于第二颗炸弹:
水平方向上有:x2=1.5Lcosθ-x0=v0t2
竖直方向上有:y2=vyt2+$\frac{1}{2}$gt22
联立可知,t1=2t2;而y2<$\frac{{y}_{3}}{2}$
则说明第二颗炸弹一定能过OO′且其与aD相交的位置一定在OO′线的右侧,则说明炸弹可能落到cd之间,包括c点.
故选:CD.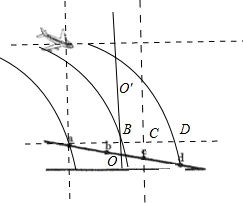
点评 本题考查平抛运动的规律,要明确水平向与竖直向的运动规律.会画草图进行分析求解.要求学生有较高的数学分析能力.

练习册系列答案
相关题目
19.由牛顿第二定律可知,无论怎样小的力都可以使物体产生加速度.可是当我们用一个很小的水平力去推很重的桌子时,却推不动它,这是因为( )
| A. | 牛顿第二定律不适用于静止物体 | |
| B. | 有加速度产生,但数值很小,不易觉察 | |
| C. | 静摩擦力大于水平推力,所以桌子静止不动 | |
| D. | 桌子所受合力为零,加速度为零,所以静止不动 |
16.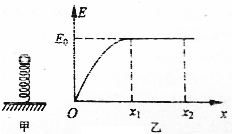 如图甲所示,竖直放置的轻弹簧一端固定在水平地面上,一小球放在轻弹簧的上端而不拴连,从静止开始向上运动的过程中,规定运动的起点为重力势能的零势能点,小球机械能E随其位移大小x的变化规律如图乙所示,且曲线与平行于x轴的直线相切,整个过程中弹簧始终在弹性限度内,不计空气阻力,则下列说法中正确的是( )
如图甲所示,竖直放置的轻弹簧一端固定在水平地面上,一小球放在轻弹簧的上端而不拴连,从静止开始向上运动的过程中,规定运动的起点为重力势能的零势能点,小球机械能E随其位移大小x的变化规律如图乙所示,且曲线与平行于x轴的直线相切,整个过程中弹簧始终在弹性限度内,不计空气阻力,则下列说法中正确的是( )
 如图甲所示,竖直放置的轻弹簧一端固定在水平地面上,一小球放在轻弹簧的上端而不拴连,从静止开始向上运动的过程中,规定运动的起点为重力势能的零势能点,小球机械能E随其位移大小x的变化规律如图乙所示,且曲线与平行于x轴的直线相切,整个过程中弹簧始终在弹性限度内,不计空气阻力,则下列说法中正确的是( )
如图甲所示,竖直放置的轻弹簧一端固定在水平地面上,一小球放在轻弹簧的上端而不拴连,从静止开始向上运动的过程中,规定运动的起点为重力势能的零势能点,小球机械能E随其位移大小x的变化规律如图乙所示,且曲线与平行于x轴的直线相切,整个过程中弹簧始终在弹性限度内,不计空气阻力,则下列说法中正确的是( )| A. | 小球在0~x1 这段位移上加速度一直减小 | |
| B. | 小球在0~x1 这段位移上加速度先减小后变大 | |
| C. | 小球在x1~x2 这段位移上先加速后减速运动 | |
| D. | 上升过程中,弹簧对小球做功为$\frac{1}{2}$E0 |
6.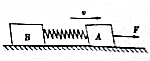 如图所示,A,B两个物体通过一轻弹簧相连,已知mA=1kg,mB=2kg,现对A施加一大小为3N的水平恒力F,使它们一起沿粗糙的水平地面向右做匀速运动,某时刻突然撤去力F.此时A,B两物体的加速度分别aA,aB,则( )
如图所示,A,B两个物体通过一轻弹簧相连,已知mA=1kg,mB=2kg,现对A施加一大小为3N的水平恒力F,使它们一起沿粗糙的水平地面向右做匀速运动,某时刻突然撤去力F.此时A,B两物体的加速度分别aA,aB,则( )
 如图所示,A,B两个物体通过一轻弹簧相连,已知mA=1kg,mB=2kg,现对A施加一大小为3N的水平恒力F,使它们一起沿粗糙的水平地面向右做匀速运动,某时刻突然撤去力F.此时A,B两物体的加速度分别aA,aB,则( )
如图所示,A,B两个物体通过一轻弹簧相连,已知mA=1kg,mB=2kg,现对A施加一大小为3N的水平恒力F,使它们一起沿粗糙的水平地面向右做匀速运动,某时刻突然撤去力F.此时A,B两物体的加速度分别aA,aB,则( )| A. | aA=aB=0 | |
| B. | aA=3m/s2,方向水平向左,aB=0 | |
| C. | aA=aB=1m/s2,方向水平向左 | |
| D. | aA=3m/s2,方向水平向右,aB=1.5m/s2,方向水平向左 |
11.一质点做直线运动,t=0时刻,v>0,a>0,此后a逐渐减小至零的过程中( )
| A. | 速度的变化越来越快 | B. | 速度逐步减小 | ||
| C. | 位移继续增大 | D. | 位移、速度始终为正值 |
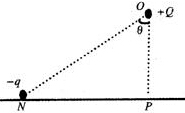 在光滑绝缘水平面的P点正上方O点固定一个电荷量为+Q的点电荷,在水平面上的N点,由静止时放质量为m,电荷量为-q的电荷,到达P点时速度为v,θ=60°,规定P点的电势为零.在+Q形成的电场中,求:
在光滑绝缘水平面的P点正上方O点固定一个电荷量为+Q的点电荷,在水平面上的N点,由静止时放质量为m,电荷量为-q的电荷,到达P点时速度为v,θ=60°,规定P点的电势为零.在+Q形成的电场中,求: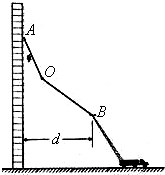 为了解决高楼救险中云梯高度不够高的问题,可在消防云梯上再伸出轻便的滑杆.被困人员使用安全带上的挂钩挂在滑杆上、沿滑杆下滑到消防云梯上逃生.通常滑杆由AO、OB两段直杆通过光滑转轴在O处连接,滑杆A端用挂钩钩在高楼的固定物上,且可绕固定物自由转动,B端用铰链固定在云梯上端,且可绕铰链自由转动,以便调节被困人员滑到云梯顶端的速度大小.设被困人员在调整好后的滑杆上下滑时滑杆与竖直方向的夹角保持不变,被困人员可看作质点、经过O点时的速度大小不变,且始终沿滑杆滑动.已知AO长L1=6m、OB长L2=12m、竖直墙与云梯上端点B的水平距离d=13.2m,被困人员安全带上的挂钩与滑杆AO间、滑杆OB间的动摩擦因数均为μ=$\frac{5}{6}$.为了安全,被困人员到达云梯顶端B点的速度不能超过6m/s,取g=10m/s2.
为了解决高楼救险中云梯高度不够高的问题,可在消防云梯上再伸出轻便的滑杆.被困人员使用安全带上的挂钩挂在滑杆上、沿滑杆下滑到消防云梯上逃生.通常滑杆由AO、OB两段直杆通过光滑转轴在O处连接,滑杆A端用挂钩钩在高楼的固定物上,且可绕固定物自由转动,B端用铰链固定在云梯上端,且可绕铰链自由转动,以便调节被困人员滑到云梯顶端的速度大小.设被困人员在调整好后的滑杆上下滑时滑杆与竖直方向的夹角保持不变,被困人员可看作质点、经过O点时的速度大小不变,且始终沿滑杆滑动.已知AO长L1=6m、OB长L2=12m、竖直墙与云梯上端点B的水平距离d=13.2m,被困人员安全带上的挂钩与滑杆AO间、滑杆OB间的动摩擦因数均为μ=$\frac{5}{6}$.为了安全,被困人员到达云梯顶端B点的速度不能超过6m/s,取g=10m/s2.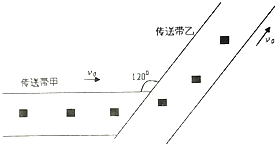 如图所示,生产车间用两个相互夹角为120°且等高的水平传送带甲和乙来传送质量为m的工件,甲的速度为v0.小工件离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0,工件与乙之间的动摩擦因数为μ,乙的宽度足够大,重力加速度为g.求:
如图所示,生产车间用两个相互夹角为120°且等高的水平传送带甲和乙来传送质量为m的工件,甲的速度为v0.小工件离开甲前与甲的速度相同,并平稳地传到乙上,乙的速度也为v0,工件与乙之间的动摩擦因数为μ,乙的宽度足够大,重力加速度为g.求: 某同学利用下列器材测定一节干电池的电动势和内电阻.
某同学利用下列器材测定一节干电池的电动势和内电阻. (满偏电流3mA,内阻10Ω)
(满偏电流3mA,内阻10Ω) (量程0~0.6A,内阻约0.1Ω)
(量程0~0.6A,内阻约0.1Ω) )
)