��Ŀ����
����Ŀ����ͼ��ʾ��A��B��C���������ֱ�Ϊ3m��2m��m�����ʵ���һ�˹̶���б�涥����һ����A��������A��B��̶�һ����ˣ�B��C����һ����ϸ�����ӣ����Ϊ![]() ��30��Ĺ⻬б��̶��ڵ����ϣ����������ϸ�߾�ƽ����б�棬��ʼϵͳ���ھ�ֹ״̬����֪�������ٶ�Ϊg����ϸ���նϵ�˲�䣬����˵����ȷ����
��30��Ĺ⻬б��̶��ڵ����ϣ����������ϸ�߾�ƽ����б�棬��ʼϵͳ���ھ�ֹ״̬����֪�������ٶ�Ϊg����ϸ���նϵ�˲�䣬����˵����ȷ����
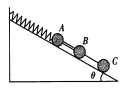
A. A��B����С��ļ��ٶȾ���б���ϣ���С��Ϊ![]()
B. B��ļ��ٶ�Ϊ![]() ��������б������
�������������
C. A��B֮��˵�������СΪmg
D. A��B֮��˵�������СΪ1.2mg
���𰸡�AD
��������AB���ն�ϸ��ǰ����A. B.C��ɵ�ϵͳΪ�о�������ϵͳ��ֹ������ƽ��״̬������Ϊ�����ɵĵ���ΪF=(3m+2m+m)gsin��=6mgsin������CΪ�о�����֪��ϸ�ߵ�����Ϊmgsin�����ն�ϸ�ߵ�˲�������ڵ��ɵ�������ͻ�������ɵ�����������A.B��ɵ�ϵͳΪ�о���������ţ�ٵڶ����ɵã�F(3m+2m)gsin��=(3m+2m)aAB
���A.B����С��ļ��ٶ�ΪaAB=gsin��/5=g/10��������б�����ϣ���A��ȷ��B������
CD����BΪ�о���������ţ�ٵڶ����ɵã�FAB2mgsin��=2ma
��ø˵�����Ϊ��FAB=1.2mg����C����D��ȷ��
��ѡ��AD��

��ϰ��ϵ�д�
�����Ŀ