题目内容
1.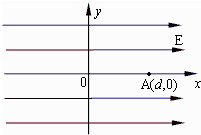 如图所示,匀强电场方向沿 轴的正方向,场强为E.在A(d,0)点有一个静止的中性微粒,由于内部作用,某一时刻突然分裂成两个质量均为 的带电微粒,同时以相同的速率朝相反的方向沿 轴开始运动.其中电荷量为-q的微粒1沿 轴负方向运动,经过一段时间到达(0,-d)点.不计重力和分裂后两微粒间的作用.试求
如图所示,匀强电场方向沿 轴的正方向,场强为E.在A(d,0)点有一个静止的中性微粒,由于内部作用,某一时刻突然分裂成两个质量均为 的带电微粒,同时以相同的速率朝相反的方向沿 轴开始运动.其中电荷量为-q的微粒1沿 轴负方向运动,经过一段时间到达(0,-d)点.不计重力和分裂后两微粒间的作用.试求(1)分裂时两个微粒的速率;
(2)当微粒1到达(0,-d)点时,电场力对微粒1做功的瞬时功率;
(3)当微粒1到达(0,-d)点时,两微粒间的距离.
分析 (1)微粒1做的是类平抛运动,根据类平抛运动的规律可以求得微粒1的速度的大小,再由动量守恒求得微粒2的速度的大小;
(2)电场力做功的瞬时功率,要用沿电场力方向的瞬时速度的大小,再由P=Fv可以求得瞬时功率的大小;
(3)画出粒子的运动轨迹,由几何知识可以求得两微粒间的距离
解答 解:(1)微粒1在y方向不受力,做匀速直线运动;在x方向由于受恒定的电场力,做匀加速直线运动.所以微粒1做的是类平抛运动.
设微粒1分裂时的速度为v1,微粒2的速度为v2则有:
在y方向上有
d=v1t
在x方向上有a=$\frac{qE}{m}$,
d=$\frac{1}{2}$at2
v1=$\sqrt{\frac{qEd}{2m}}$
速度方向沿y轴的负方向.
中性微粒分裂成两微粒时,遵守动量守恒定律,有
mv1+mv2=0
所以 v2=-v1
所以 v2的大小为 $\sqrt{\frac{qEd}{2m}}$,方向沿y正方向.
(2)设微粒1到达(0,-d)点时的速度为VB,则电场力做功的瞬时功率为,
P=qEVB cosθ=qEVBx,
其中由运动学公式 VBx=$\sqrt{2ad}$=$\sqrt{\frac{2qEd}{m}}$,
所以 P=qE$\sqrt{\frac{2qEd}{m}}$,
(3)两微粒的运动具有对称性,如图所示,当微粒1到达(0,-d)点时发生的位移 S1=$\sqrt{2}$d,
则当微粒1到达(0,-d)点时,两微粒间的距离为BC=2S1=2$\sqrt{2}$d.
答:(1)分裂时微粒1的速度大小为$\sqrt{\frac{qEd}{2m}}$,方向沿着y轴的负方向;微粒2的速度大小为$\sqrt{\frac{qEd}{2m}}$,方向沿着y轴的正方向;
(2)当微粒1到达(0,-d)点时,电场力对微粒1做功的瞬间功率是 qE$\sqrt{\frac{2qEd}{m}}$;
(3)当微粒1到达(0,-d)点时,两微粒间的距离是2$\sqrt{2}$d
点评 带电微粒在电场中运动,一般不考虑重力的作用,只是受到电场力的作用,再进一步判断微粒的运动情况,本题中微粒做类平抛运动,由类平抛运动的规律就可以求得速度,在计算功率时一定要注意求的是瞬时功率,注意公式的选择

 阅读快车系列答案
阅读快车系列答案 如图所示为卢瑟福α粒子散射实验装置的示意图,图中的显微镜可在圆周轨道上转动,通过显微镜前相连的荧光屏可观察α粒子在各个角度的散射情况.下列说法中正确的是( )
如图所示为卢瑟福α粒子散射实验装置的示意图,图中的显微镜可在圆周轨道上转动,通过显微镜前相连的荧光屏可观察α粒子在各个角度的散射情况.下列说法中正确的是( )| A. | 相同时间内放在A位置时观察到屏上的闪光次数最多 | |
| B. | 相同时间内放在B位置时观察到屏上的闪光次数比放在A位置时少得多 | |
| C. | 放在C、D位置时屏上观察不到闪光 | |
| D. | 放在D位置时屏上仍能观察到一些闪光,但次数极少 |
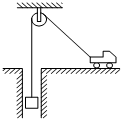
| A. | 匀速上升 | |
| B. | 加速上升 | |
| C. | 减速上升 | |
| D. | 无法确定运动速度是匀速、加速还是减速 |
| A. | 电场线是电荷移动的轨迹 | |
| B. | 电场线不可能与运动轨迹重合 | |
| C. | 仅受电场力作用时,电荷不可能沿电场线运动 | |
| D. | 电荷的运动轨迹有可能与电场线重合 |
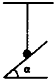 如图所示,小球用细绳系住,细绳被竖直拉紧,小球与光滑斜面接触并处于静止状态,则小球受力情况是( )
如图所示,小球用细绳系住,细绳被竖直拉紧,小球与光滑斜面接触并处于静止状态,则小球受力情况是( )| A. | 重力、绳对球的拉力 | |
| B. | 重力、绳对球的拉力、斜面的弹力 | |
| C. | 重力、斜面的弹力 | |
| D. | 重力、绳对球的拉力、斜面对球的摩擦力 |
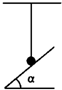 如图所示,小球用细绳系住,细绳被竖直拉紧,小球与光滑斜面接触并处于静止状态,则小球受力情况是( )
如图所示,小球用细绳系住,细绳被竖直拉紧,小球与光滑斜面接触并处于静止状态,则小球受力情况是( )| A. | 重力、绳对球的拉力 | |
| B. | 重力、绳对球的拉力、斜面的弹力 | |
| C. | 重力、斜面对球的弹力 | |
| D. | 重力、绳对球的拉力、斜面对球的摩擦力 |
 轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小球,电梯中有质量为50kg的乘客如图所示,在电梯运行时乘客发现轻质弹簧的伸长量是电梯静止时的一半,取g=10m/s2这一现象表明( )
轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小球,电梯中有质量为50kg的乘客如图所示,在电梯运行时乘客发现轻质弹簧的伸长量是电梯静止时的一半,取g=10m/s2这一现象表明( )| A. | 电梯此时可能正以1m/s2的加速度大小加速上升,也可能是以1m/s2的加速度大小减速上升 | |
| B. | 电梯此时不可能是以1m/s2的加速度大小减速上升,只能是以5m/s2的加速度大小加速下降 | |
| C. | 电梯此时可能正以5m/s2的加速度大小加速下降,也可能是以5m/s2的加速度大小减速上升 | |
| D. | 不论电梯此时是上升还是下降,加速还是减速,乘客对电梯地板的压力大小一定是250N |