题目内容
16.在月球表面上,以初速度v0竖直上抛一个小球,经过时间t落回到抛出点,已知月球的半径为R,则月球的质量为$\frac{2{V}_{0}{R}^{2}}{Gt}$(不计阻力).分析 运用竖直上抛运动规律求出月球表面重力加速度.忽略月球自转的影响,根据万有引力等于重力列出等式求解月球的质量M
解答 解:设月球表面的重力加速度为g,则据竖直上抛运动可知:g=$\frac{2{V}_{0}}{t}$
又因为在月球表面,物体受到的重力等于月球对他的万有引力G$\frac{Mm}{{R}^{2}}$=mg
其中M为月球的质量
所以月球的质量为M=$\frac{2{V}_{0}{R}^{2}}{Gt}$
故答案为:$\frac{2{V}_{0}{R}^{2}}{Gt}$
点评 重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.本题要求掌握物体所受重力等于万有引力这个重要的关系

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
6.下列说法中正确的是( )
| A. | 质点、位移都是理想化模型 | B. | 参考系只能选地面 | ||
| C. | 第3秒末指的是时刻 | D. | 第3秒内指的是时刻 |
4.一艘小船在100m宽的河中横渡到对岸,已知水流速度为3m/s,小船在静水中速度为4m/s,则( )
| A. | 小船渡河的最短时间为20s | B. | 小船渡河的最短时间为25s | ||
| C. | 小船渡河的最短位移为125m | D. | 小船渡河的最短位移为100m |
11.一质点做圆周运动,速度处处不为零,则( )
| A. | 任意何时刻质点所受的向心力一定不为零 | |
| B. | 任意何时刻质点的加速度一定不为零 | |
| C. | 质点速度的大小一定不断地变化 | |
| D. | 质点速度地方向一定不断地变化 |
5.某物体运动的v-t图象如图所示,则该物体在0~t0时间内( )
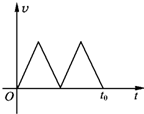

| A. | 做往复运动 | B. | 做匀速直线运动 | ||
| C. | 沿某一方向做直线运动 | D. | 以上说法均不正确 |
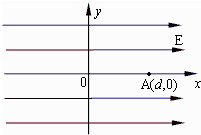 如图所示,匀强电场方向沿 轴的正方向,场强为E.在A(d,0)点有一个静止的中性微粒,由于内部作用,某一时刻突然分裂成两个质量均为 的带电微粒,同时以相同的速率朝相反的方向沿 轴开始运动.其中电荷量为-q的微粒1沿 轴负方向运动,经过一段时间到达(0,-d)点.不计重力和分裂后两微粒间的作用.试求
如图所示,匀强电场方向沿 轴的正方向,场强为E.在A(d,0)点有一个静止的中性微粒,由于内部作用,某一时刻突然分裂成两个质量均为 的带电微粒,同时以相同的速率朝相反的方向沿 轴开始运动.其中电荷量为-q的微粒1沿 轴负方向运动,经过一段时间到达(0,-d)点.不计重力和分裂后两微粒间的作用.试求 某实验室提供的实验器材如下:
某实验室提供的实验器材如下: