��Ŀ����
����Ŀ����ͼ��O��A��BΪͬһ��ֱƽ���ڵ������㣬����������ɵ���ֱ�������Ρ�OAB����һ����Ϊm��С����һ���ij�������O��ˮƽ�����׳���С�����˶�������ͨ��A�㡣ʹ��С������磬�����Ϊ-q��ͬʱ��һ��ǿ�糡����ǿ�������OAB����ƽ��ƽ�С��ִ�O����ͬ���ij�������ijһ�����׳��˴���С��С��ͨ����A�㣬����A��ʱ�Ķ����dz����ܵ�![]() ��������С���O����ͬ���ij���������һ�����׳���ͨ��B�㣬�ҵ���B��ʱ�Ķ���Ϊ�����ܵ�9�����������ٶȴ�СΪg����
��������С���O����ͬ���ij���������һ�����׳���ͨ��B�㣬�ҵ���B��ʱ�Ķ���Ϊ�����ܵ�9�����������ٶȴ�СΪg����
��1���糡ʱ��С��A��ʱ�Ķ���������ܵı�ֵ��
��2���糡ǿ�ȵĴ�С�ͷ���

���𰸡���1��![]() ��2��
��2��![]() ����������ֱ�����75�㡣
����������ֱ�����75�㡣
��������
��1��С����ƽ���˶�������ٶ�v0��������EK0����O��AB���˶�ʱ��Ϊt����O��A����ֱ����Ϊd��
ˮƽ����
![]()
��ֱ����
![]()
���
![]()
���ݶ��ܶ�����֪С��Aʱ�Ķ���Ϊ
EKA![]() ��
��
����
![]()
��2���ӵ糡��O�㵽A���½���d����O�㵽B��������d���������غ㣬�����ܼ�����
![]()
![]()
����ǿ�糡�У���������ֱ�ߣ����ƵĽ����Ǿ��ȵģ���ͼ��ʾ��
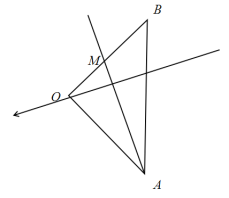
��ֱ��OB�ϵ�M��ĵ�����A�ĵ�����ͬ��M�㵽O��ľ�����x����ͼ������
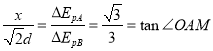
���
![]() ��
��
MA�ǵ����ߣ��糡����MA�Ĵ���OCƽ�У���OAM=30����
��糡ǿ�ȵĴ�С��E����
![]()
���
![]() ��
��
��������ֱ�����75����











