题目内容
【题目】如图所示，在倾角θ=37°的斜面上有一块竖直放置的挡板，在挡板和斜面之间放有一个光滑圆球，当系统静止时挡板上的压力为20N，sin37°=0.6，cos37°=0.8，重力加速度g=10m/s2 ． 试求：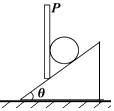
（1）球对斜面的压力和圆球的重力．
（2）要让挡板压力恰好为零，整个装置在水平方向上将怎样运动？
【答案】
（1）解：球受重力、挡板支持力、斜面支持力，按照作用效果，将重力沿着垂直挡板和垂直斜面方向分解，如图所示：
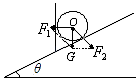
结合几何知识可得： 
；
球对斜面的压力大小为： 
；
答：球对斜面的压力大小为 
，圆球的重力大小为 
．
（2）解：对球受力分析，受重力和支持力，合力水平，如图所示：
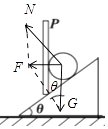
合力：F=Gtanθ，
根据牛顿第二定律，有：F=ma，
解得：a=gtanθ=10× 
=7.5m/s2，水平向左，
故系统向左以7.5m/s2的加速度匀加速直线运动，或者向右以7.5m/s2的加速度做匀减速直线运动．
答：要让挡板压力恰好为零，整个装置向左以7.5m/s2的加速度匀加速直线运动，或者向右以7.5m/s2的加速度做匀减速直线运动．
【解析】（1）球受重力、挡板支持力、斜面支持力，将重力沿着垂直挡板和垂直斜面方向分解，根据几何知识进行解答；（2）对球受力分析，受重力和支持力，合力水平，根据牛顿第二定律列方程求解加速度大小，再分析系统的运动情况．
【考点精析】根据题目的已知条件，利用力的合成的相关知识可以得到问题的答案，需要掌握求几个已知力的合力，叫做力的合成；共点的两个力（F 1 和F 2 ）合力大小F的取值范围为:|F 1 -F 2 |≤F≤F 1 +F 2．
练习册系列答案
相关题目
