题目内容
 如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.已知小球质量为m,重力加速度为g,忽略圆管内径,两小球可视为质点,空气阻力及各处摩擦均不计,求:
如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.已知小球质量为m,重力加速度为g,忽略圆管内径,两小球可视为质点,空气阻力及各处摩擦均不计,求:(1)粘合后的两球从飞出轨道时的速度v;
(2)碰撞前瞬间,小球A对圆管的力;
(3)小球A冲进轨道时速度vA的大小.
分析:(1)粘合后的两球飞出轨道后做平抛运动,根据高度2R和水平距离2R求出速度v.
(2)根据动量守恒定律求出碰撞前瞬间小球A的速度.碰撞前由重力和轨道的支持力提供A的向心力,由牛顿第二定律求出轨道的支持力,由牛顿第三定律求解小球A对圆管的压力.
(3)小球A冲进轨道过程中,只有重力做功,其机械能守恒,由机械能守恒定律求出小球A冲进轨道时速度vA的大小.
(2)根据动量守恒定律求出碰撞前瞬间小球A的速度.碰撞前由重力和轨道的支持力提供A的向心力,由牛顿第二定律求出轨道的支持力,由牛顿第三定律求解小球A对圆管的压力.
(3)小球A冲进轨道过程中,只有重力做功,其机械能守恒,由机械能守恒定律求出小球A冲进轨道时速度vA的大小.
解答:解:(1)粘合后的两球飞出轨道后做平抛运动,则有:2R=
gt2
解得:t=2
平抛运动的初速度为:v=
=
(2)根据动量守恒,两球碰撞过程有:
mv1=2mv
碰前对A有:N+mg=m
解得:N=3mg
根据牛顿第三定律,小球A对圆管的压力大小为3mg,方向竖直向上.
(3)小球A在圆管内运动过程,机械能守恒:
mv2=
mv12+mg2R
解得:v=2
答:
(1)粘合后的两球从飞出轨道时的速度v=
;
(2)碰撞前瞬间,小球A对圆管的力为3mg;
(3)小球A冲进轨道时速度vA的大小为2
.
| 1 |
| 2 |
解得:t=2
|
平抛运动的初速度为:v=
| 2R |
| t |
| gR |
(2)根据动量守恒,两球碰撞过程有:
mv1=2mv
碰前对A有:N+mg=m
| v12 |
| R |
解得:N=3mg
根据牛顿第三定律,小球A对圆管的压力大小为3mg,方向竖直向上.
(3)小球A在圆管内运动过程,机械能守恒:
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=2
| 2gR |
答:
(1)粘合后的两球从飞出轨道时的速度v=
| gR |
(2)碰撞前瞬间,小球A对圆管的力为3mg;
(3)小球A冲进轨道时速度vA的大小为2
| 2gR |
点评:本题是平抛运动,动量守恒和机械能守恒定律等知识的综合应用,按程序法进行分析,要抓住两个过程间速度的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的质量为m的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求:
如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的质量为m的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求: 如图所示,圆管构成的半圆轨道竖直固定在水平面上,半径为R,直径比管内径略小的小球A,以某一初速冲进轨道,到达最高点M时与静止在该处的质量相同的小球B发生碰撞,然后粘在一起飞出轨道,落地点距离N点为2R,重力加速度为g,忽略管的内径和一切阻力,求:
如图所示,圆管构成的半圆轨道竖直固定在水平面上,半径为R,直径比管内径略小的小球A,以某一初速冲进轨道,到达最高点M时与静止在该处的质量相同的小球B发生碰撞,然后粘在一起飞出轨道,落地点距离N点为2R,重力加速度为g,忽略管的内径和一切阻力,求: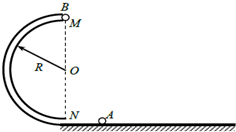 如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径R为5m,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度V0从N点冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生弹性碰撞,碰后A、B两球交换速度,B球水平飞出轨道,落地点距N点距离为10m;A球从最高点初速度为零沿原路返回,水平地面的动摩擦系数μ为0.5.重力加速度g取10m/s2,忽略圆管内径,空气阻力及圆管内部摩擦不计,求:
如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径R为5m,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度V0从N点冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生弹性碰撞,碰后A、B两球交换速度,B球水平飞出轨道,落地点距N点距离为10m;A球从最高点初速度为零沿原路返回,水平地面的动摩擦系数μ为0.5.重力加速度g取10m/s2,忽略圆管内径,空气阻力及圆管内部摩擦不计,求: (2010?南京模拟)如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M后飞出轨道,落地点到N点的距离为4R.忽略圆管内径,不计空气阻力及各处摩擦,已知重力加速度为g.求:
(2010?南京模拟)如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M后飞出轨道,落地点到N点的距离为4R.忽略圆管内径,不计空气阻力及各处摩擦,已知重力加速度为g.求: