题目内容
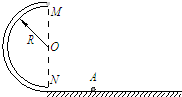 (2010?南京模拟)如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M后飞出轨道,落地点到N点的距离为4R.忽略圆管内径,不计空气阻力及各处摩擦,已知重力加速度为g.求:
(2010?南京模拟)如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M后飞出轨道,落地点到N点的距离为4R.忽略圆管内径,不计空气阻力及各处摩擦,已知重力加速度为g.求:(1)小球从飞出轨道到落地的时间t.
(2)小球从M点飞出时的速度大小v.
(3)小球在轨道最低点N时对轨道的压力F.
分析:(1)小球飞出轨道后做平抛运动,根据平抛运动的竖直分位移公式列式求解即可;
(2)小球飞出轨道后做平抛运动,再根据平抛运动的水平分位移公式列式求解;
(3)先根据机械能守恒定律求出小球经过N点的速度,再对小球在N点运用牛顿第二定律和向心力公式列式求解.
(2)小球飞出轨道后做平抛运动,再根据平抛运动的水平分位移公式列式求解;
(3)先根据机械能守恒定律求出小球经过N点的速度,再对小球在N点运用牛顿第二定律和向心力公式列式求解.
解答:解:(1)小球飞出轨道后做平抛运动,竖直方向分运动为自由落体运动,有:
2R=
gt2
解得
t=
即小球从飞出轨道到落地的时间t等于
.
(2)小球飞出轨道后做平抛运动,水平方向分运动为匀速直线运动,有
4R=vt
解得
v=
=2
即小球从M点飞出时的速度大小v等于2
.
(3)小球从N到M过程机械能守恒,由机械能守恒定律知:
m
=mg(2R)+
m
解得
=
=2
在N点,重力和支持力的合力提供小球做圆周运动的向心力,有
N-mg=m
解得
N=9mg
故小球在轨道最低点N时对轨道的压力F等于9mg.
2R=
| 1 |
| 2 |
解得
t=
|
即小球从飞出轨道到落地的时间t等于
|
(2)小球飞出轨道后做平抛运动,水平方向分运动为匀速直线运动,有
4R=vt
解得
v=
| 4R |
| t |
| gR |
即小球从M点飞出时的速度大小v等于2
| gR |
(3)小球从N到M过程机械能守恒,由机械能守恒定律知:
| 1 |
| 2 |
| v | 2 N |
| 1 |
| 2 |
| v | 2 M |
解得
| v | N |
|
| 2gR |
在N点,重力和支持力的合力提供小球做圆周运动的向心力,有
N-mg=m
| ||
| R |
解得
N=9mg
故小球在轨道最低点N时对轨道的压力F等于9mg.
点评:本题关键要分析小球的运动情况,然后分阶段运用平抛运动的分位移公式、机械能守恒定律和向心力公式列式求解.

练习册系列答案
相关题目
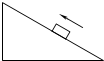 (2010?南京模拟)如图所示,物体以一定的初速度在粗糙斜面上向上滑行过程中,关于物体的受力情况,下列说法中正确的是( )
(2010?南京模拟)如图所示,物体以一定的初速度在粗糙斜面上向上滑行过程中,关于物体的受力情况,下列说法中正确的是( )