题目内容
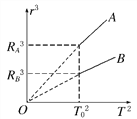
【题目】假设宇宙中有两颗相距无限远的行星A和B，半径分别为RA和RB。两颗行星周围卫星的轨道半径的三次方(r3)与运行周期的平方(T2)的关系如图所示，T0为卫星环绕行星表面运行的周期。则( )
A. 行星A的质量小于行星B的质量
B. 行星A的密度小于行星B的密度
C. 行星A的第一宇宙速度等于行星B的第一宇宙速度
D. 当两行星的卫星轨道半径相同时，行星A的卫星向心加速度大于行星B的卫星向心加速度
【答案】D
【解析】A、根据万有引力提供向心力,有：
，解得
，对于环绕行星A表面运行的卫星，有：
，对于环绕行星B表面运行的卫星，有
，联立解得
，由图知 
，所以
，故A错误；
B、A行星质量为：
，B行星的质量为：
，代入解得
，解得
，故B错误；
C、行星的近地卫星的线速度即第一宇宙速度，根据万有引力提供向心力，有：
，解得
，因为，所以
，故C错误；
D、根据
知，
，由于，行星运动的轨道半径相等，则行星A的卫星的向心加速度大于行星B的卫星的向心加速度，故D正确；
故选D。
练习册系列答案
相关题目
