题目内容
10.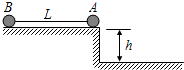 如图所示,质量mA=2kg和mB=3kg的小球A、B(可视为质点)用细线相连,放在高h=0.5m的水平桌面上,A球刚好在桌边,细线恰好伸直且其长度大于桌面高度、现使小球A由静止开始下落,由于光滑曲面挡板的存在,小球B从桌边滑落时速度大小不变而方向变为竖直向下.若A、B两球落地后均不再弹起,不计一切摩擦,取g=10m/s2,求:
如图所示,质量mA=2kg和mB=3kg的小球A、B(可视为质点)用细线相连,放在高h=0.5m的水平桌面上,A球刚好在桌边,细线恰好伸直且其长度大于桌面高度、现使小球A由静止开始下落,由于光滑曲面挡板的存在,小球B从桌边滑落时速度大小不变而方向变为竖直向下.若A、B两球落地后均不再弹起,不计一切摩擦,取g=10m/s2,求:(1)A、B两球落地时各自的速率.
(2)绳子拉力对B球做的功.
分析 (1)把AB看成一个整体,根据牛顿第二定律求出加速度,再根据位移速度公式求解;B下落的过程中机械能守恒,由此即可求出B的速度;
(2)A落地时,B的速度与A球速度相等,对B,根据动能定理求出绳子对B拉力做的功;
解答 解:(1)把AB看成一个整体,根据牛顿第二定律得:
a=$\frac{{m}_{A}g}{{m}_{A}+{m}_{B}}=\frac{20}{5}=4m/{s}^{2}$,
则A球落地时的速率为:v=$\sqrt{2ah}=\sqrt{2×4×0.5}=2m/s$
A落地后只有重力对B做功,B的机械能守恒,则:
$\frac{1}{2}{m}_{B}{v}^{2}+{m}_{B}gh=\frac{1}{2}{m}_{B}{v}_{B}^{2}$
代入数据得:${v}_{B}=\sqrt{14}$m/s
(2)A落地时,B的速度与A球速度相等,即:v=2m/s,
对B,根据动能定理得轻绳的拉力对B球做的功为:W=$\frac{1}{2}{m}_{B}{v}^{2}=\frac{1}{2}×3×4=6J$
答:(1)A、B两球落地时各自的速率分别为2m/s和$\sqrt{14}$m/s.
(2)绳子拉力对B球做的功是6J.
点评 本题主要考查了牛顿第二定律、运动学基本公式、动能定理等的直接应用,要求同学们能正确分析物体的运动情况和受力情况.

练习册系列答案
相关题目
20.压力传感器可以用在( )
| A. | 空调温度控制器 | B. | 燃气泄露报警器 | C. | 电梯超载报警器 | D. | 酒精浓度测试仪 |
1.伞兵在抢险中具有重要作用,是精锐中的精锐;在一次低空跳伞训练中,当直升机悬停在离地面224m高处时,伞兵离开直升机做自由落体运动,经过一段时间后,打开降落伞,展开伞后伞兵以12.5m/s2的加速度匀减速下降;为了伞兵的安全,要求伞兵落地速度不超过5m/s,取重力加速度为g=10m/s2,根据上述信息,下列说法正确的是( )
| A. | 伞兵展伞时,最大速度为40m/s | |
| B. | 伞兵展伞时,离地面的高度至少为99m | |
| C. | 伞兵下落过程中的机械能先不变后减小 | |
| D. | 可以求出伞兵匀减速下落过程中克服阻力做的功 |
15. 如图所示,由两块相互靠近的平行金属板组成的平行板电容器的极板N与静电计相接,极板M接地,静电计的外壳也接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距一定距离d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q不变,下面哪些操作将使静电计指针张角变小( )
如图所示,由两块相互靠近的平行金属板组成的平行板电容器的极板N与静电计相接,极板M接地,静电计的外壳也接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距一定距离d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q不变,下面哪些操作将使静电计指针张角变小( )
 如图所示,由两块相互靠近的平行金属板组成的平行板电容器的极板N与静电计相接,极板M接地,静电计的外壳也接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距一定距离d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q不变,下面哪些操作将使静电计指针张角变小( )
如图所示,由两块相互靠近的平行金属板组成的平行板电容器的极板N与静电计相接,极板M接地,静电计的外壳也接地.用静电计测量平行板电容器两极板间的电势差U.在两板相距一定距离d时,给电容器充电,静电计指针张开一定角度.在整个实验过程中,保持电容器所带电量Q不变,下面哪些操作将使静电计指针张角变小( )| A. | 将M板向下平移 | B. | 将M板沿水平向右方向靠近N板 | ||
| C. | 在M、N之间插入云母板 | D. | 将M板向上移动的同时远离N板 |
2. 在探究“质量一定,加速度a与合外力F的关系”实验中.
在探究“质量一定,加速度a与合外力F的关系”实验中.
某学生根据实验数据作出了如图所示的a-F图象,其中图线不过原点并在末端发生了弯曲,产生这种现象的原因可能有( )
 在探究“质量一定,加速度a与合外力F的关系”实验中.
在探究“质量一定,加速度a与合外力F的关系”实验中.某学生根据实验数据作出了如图所示的a-F图象,其中图线不过原点并在末端发生了弯曲,产生这种现象的原因可能有( )
| A. | 在平衡摩擦力时,木板一端垫起的高度偏大 | |
| B. | 在平衡摩擦力时,木板一端垫起的高度偏小 | |
| C. | 盘和重物 的总质量m远小于车和砝码的总质量M | |
| D. | 盘和重物的总质量m不远小于车和砝码的总质量M |
20.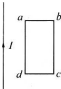 如图所示,通电导线与矩形线圈处于同一平面,下列做法一定能使线圈产生感应电流的是( )
如图所示,通电导线与矩形线圈处于同一平面,下列做法一定能使线圈产生感应电流的是( )
 如图所示,通电导线与矩形线圈处于同一平面,下列做法一定能使线圈产生感应电流的是( )
如图所示,通电导线与矩形线圈处于同一平面,下列做法一定能使线圈产生感应电流的是( )| A. | 导线中电流不变,将线圈向上平动 | |
| B. | 导线中电流变小,将线圈向右平动 | |
| C. | 导线中电流变大,将线圈向右平动 | |
| D. | 导线中电流不变,线圈以ab边为轴转动时(小于90°) |
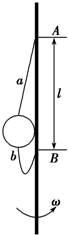 如图所示,半径为$\frac{l}{4}$、质量为m的小球用两根不可伸长的轻绳a、b连接(绳子的延长线经过球心 ),两轻绳的另一端系在一根竖直杆的A、B两点上,A、B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l.当竖直杆以自己为轴转动并达到稳定时(轻绳a、b与杆在同一竖直平面内).求:
如图所示,半径为$\frac{l}{4}$、质量为m的小球用两根不可伸长的轻绳a、b连接(绳子的延长线经过球心 ),两轻绳的另一端系在一根竖直杆的A、B两点上,A、B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l.当竖直杆以自己为轴转动并达到稳定时(轻绳a、b与杆在同一竖直平面内).求: 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A,半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B,用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来,杆和半圆形轨道在同一竖直面内,两小球均可看做质点,且不计滑轮大小的影响,(g=10m/s2),现给小球A一个水平向右的恒力F=55N.求:
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A,半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B,用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来,杆和半圆形轨道在同一竖直面内,两小球均可看做质点,且不计滑轮大小的影响,(g=10m/s2),现给小球A一个水平向右的恒力F=55N.求: 在探究“加速度与力、质量的关系”实验中,小明分别用物体A、B做了加速度随着外力的变化关系实验,如图(1)所示,用不同的重物P分别挂在光滑的动滑轮拉物体A、B,处理数据后,他们得到加速度a与弹簧秤弹力F的关系图象如图(2)所示,由图象可知
在探究“加速度与力、质量的关系”实验中,小明分别用物体A、B做了加速度随着外力的变化关系实验,如图(1)所示,用不同的重物P分别挂在光滑的动滑轮拉物体A、B,处理数据后,他们得到加速度a与弹簧秤弹力F的关系图象如图(2)所示,由图象可知