Question

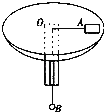
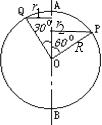
【题目】一圆环，其圆心为O，若以它的直径AB为轴做匀速转动，如图所示：

（1）圆环上P、Q两点的线速度大小之比是；
（2）若圆环的半径是20cm，绕AB轴转动的周期是πs，环上Q点的向心加速度大小是m/s2 ．

Answer 1

【答案】
（1） ：1
（2）0.4
【解析】解：P、Q两点以它的直径AB为轴做匀速转动，它们的角速度相同都为ω，

所以Q点转动的半径r1=Rsin30°= R，

P点转动的半径r2=Rsin60°= R

根据v=ωr得：

=

即圆环上P、Q两点的线速度大小之比是 ：1

根据a= 得：

Q点的向心加速度大小为：a=0.4m/s2．

所以答案是： ：1，0.4

【考点精析】关于本题考查的匀速圆周运动和向心力，需要了解匀速圆周运动线速度的大小恒定，角速度、周期和频率都是恒定不变的，向心加速度和向心力的大小也都是恒定不变的，是速度大小不变而速度方向时刻在变的变速曲线运动；向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力才能得出正确答案．