题目内容
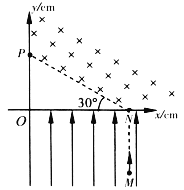
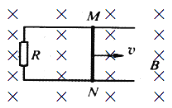
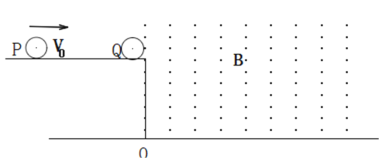
【题目】如图所示,在光滑水平平台右侧空间,存在着范围无限大,磁感应强度为B,方向垂直纸面向外的匀强磁场。平台右端放一个质量为m,带负电-q的小球Q,左侧有一个质量为M=4m,不带电的绝缘小球P,以水平初速度![]() 正对Q向右运动发生正碰,撞过程中没有机械能损失且电荷量不发生转移。已知水平平台距地面的高度为h,重力加速度为g,不计空气阻力。求:
正对Q向右运动发生正碰,撞过程中没有机械能损失且电荷量不发生转移。已知水平平台距地面的高度为h,重力加速度为g,不计空气阻力。求:
(1)P、Q两球发生弹性正碰后速度分别为多少?
(2)碰后小球P落地点到平台右端的水平距离x为多少?
(3)碰后小球Q电量不变,在重力和磁场力作用下运动,求小球Q碰后离地面的最大高度H为多少?此时小球Q的速度v为多少?
【答案】(1)![]() ,
,![]() ,方向均向右;(2)
,方向均向右;(2)![]() ;(3)
;(3)![]() ,
,![]() 。
。
【解析】
(1)设向右为正方向,则据动量守恒定律可得:
Mv0=Mv1+mv2
根据能量守恒定律得:
![]()
由以上两式解得:
P球的速度:![]() ,方向向右;
,方向向右;
Q球的速度![]() ,方向向右;
,方向向右;
(2)碰后小球P做平抛运动,由平抛规律得:
水平方向:
x =v1t
竖直方向:
![]()
由上述二式联立求得:
![]()
(3)碰后小球Q离开平台,受竖直向下的重力和竖直向上的洛伦兹力。Q球的速度可分解为:
![]()
即可看作以v0速度向右匀速直线运动和以![]() 逆时针圆周运动的合运动。由
逆时针圆周运动的合运动。由
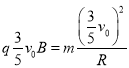
得
![]()
则小球Q碰后离地面的最大高度H为
![]()
此时小球Q的速度v为:
![]() 。
。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目