题目内容
14. 如图所示,两个相同的木板A、B置于水平地面上,质量均为m=1kg,其中B固定不动,A可以沿地面滑动,它们相距s=1.5m.质量为2m,大小可忽略的物块C置于A板的左端.C与A之间的动摩擦因数为μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力.现给C施加一个水平向右,大小为0.4mg的水平恒力F,使其开始运动,设A与B发生碰撞后立即静止,重力加速度g=10m/s2.求
如图所示,两个相同的木板A、B置于水平地面上,质量均为m=1kg,其中B固定不动,A可以沿地面滑动,它们相距s=1.5m.质量为2m,大小可忽略的物块C置于A板的左端.C与A之间的动摩擦因数为μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力.现给C施加一个水平向右,大小为0.4mg的水平恒力F,使其开始运动,设A与B发生碰撞后立即静止,重力加速度g=10m/s2.求 (1)要使C最终不脱离木板,每块木板的长度至少应为多少?
(2)若C恰好没有脱离木板,水平恒力F所做的功.
分析 (1)C与木板间的滑动摩擦力 f1=μ1×2mg=0.44 mg>F=0.4mg,说明A和C能保持相对静止,在F的作用下一起向右匀加速运动,由动能定理求出A刚要与B发生碰撞时的速度.A与B发生碰撞后停止,C在木板上做匀减速直线运动,若刚好滑到B的最右端恰好停止,则木板的长度最小.对C物体,由动能定理可求木板的最小长度.
(2)C恰好没有脱离木板,C的位移为 sC=s+2L,根据W=FsC求F做的功.
解答 解:(1)由于C与木板间的滑动摩擦力 f1=μ1×2mg=0.44 mg>F=0.4 mg
所以,A和C能保持相对静止.
在F的作用下一起向右匀加速运动,设A刚要与B发生碰撞时的速度为v,对AC整体,由动能定理得
(F-3μ2mg)s=$\frac{1}{2}×3m{v}^{2}$
解得 v=1 m/s.
A与B发生碰撞后停止,C在木板上做匀减速直线运动,若刚好滑到B的最右端恰好停止,则木板的长度最小.对C物体,由动能定理得
(F-μ1×2mg)×2L=-$\frac{1}{2}×2m{v}^{2}$
解得 L=1.25 m,即每块木板的长度至少应为1.25 m.
(2)C恰好没有脱离木板,C的位移为 sC=s+2L=4m.
故水平恒力F所做的功为 W=FsC=16J
答:
(1)要使C最终不脱离木板,每块木板的长度至少应为1.25m;
(2)若C恰好没有脱离木板,水平恒力F所做的功为16J.
点评 本题是多体多过程的问题,要在分析清楚物体运动情况的基础上,准确选择解题规律,明确涉及力在空间的效果时,运用动能定理求速度或位移.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
5.在物理学的重大发现中科学家们创造出了许多物理学研究方法,如理想实验法、控制变量法、极限思维法、类比法和科学假说法、建立理想模型法、微元法等等,以下叙述正确的是( )
| A. | 在定义加速度,电场强度,电容器的电容等物理量时采用了类比法 | |
| B. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| C. | 在用实验探究加速度、力和质量三者之间关系时,应用了控制变量法 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
2.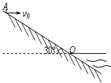 如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
 如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )| A. | 若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越大 | |
| B. | 若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越小 | |
| C. | 若石块能落入水中,则v0越大,落水时速度方向与水平面的夹角越大 | |
| D. | 若v0=18m/s,则石块可以落入水中 |
9.下列说法正确的是( )
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 理想气体绝热压缩内能会增大 | |
| C. | 理想气体等温膨胀内能会减小 | |
| D. | 热量不可以从低温物体传到高温物体 |
19.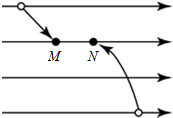 如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
 如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )
如图所示的水平匀强电场中,将两个带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,不计重力,则( )| A. | M的带电量比N的大 | B. | M带负电荷,N带正电荷 | ||
| C. | 静止时M受到的合力比N的大 | D. | 移动过程中匀强电场对M做负功 |
6. 把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
 把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )| A. | A端的电势比B端的电势高 | |
| B. | A端的电荷比B端的电荷密集 | |
| C. | A端额电势可能比B端的电势高,也可能比B端的电势低 | |
| D. | A端的电势与B端的电势相等 |
3.在伽利略的斜面实验中,如果空气阻力和摩擦阻力不能忽略不计,则下列说法正确的是( )
| A. | 动能和势能之和仍守恒 | |
| B. | 动能和势能之和将增大 | |
| C. | 动能和势能之和将逐渐减小,但总的能量还是守恒的 | |
| D. | 以上说法均不对 |
5. 如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )
如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )
 如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )
如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )| A. | 场强大小关系满足E2=2E1 | |
| B. | 场强E1一定小于E2 | |
| C. | 若AB高度差为h,则UAB=-$\frac{mgh}{q}$ | |
| D. | 带电小球在AB间运动电势能不断减少 |
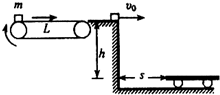 如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求:
如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求: