题目内容
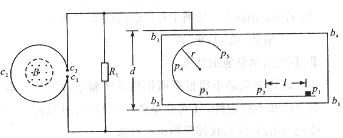
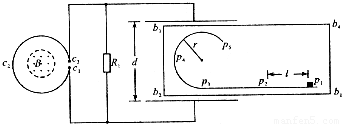
如图所示,直线形挡板p1p2p3与半径为r的圆弧形挡板p3p4p5平滑连接并安装在水平台面b1b2b3b4上,挡板与台面均固定不动.线圈c1c2c3的匝数为n,其端点c1、c3通过导线分别与电阻R1和平行板电容器相连,电容器两极板间的距离为d,电阻R1的阻值是线圈c1c2c3阻值的2倍,其余电阻不计,线圈c1c2c3内有一面积为S、方向垂直于线圈平面向上的匀强磁场,磁场的磁感应强度B随时间均匀增大.质量为m的小滑块带正电,电荷量始终保持为q,在水平台面上以初速度v从p1位置出发,沿挡板运动并通过p5位置.若电容器两板间的电场为匀强电场,p1、p2在电场外,间距为L,其间小滑块与台面的动摩擦因数为μ,其余部分的摩擦不计,重力加速度为g.求:
(1)小滑块通过p2位置时的速度大小.
(2)电容器两极板间电场强度的取值范围.
(3)经过时间t,磁感应强度变化量的取值范围.
【答案】分析:(1)根据过程分析,滑块从p1运动到p2的过程运用动能定理可以求解第一问;
(2)小滑块要能到达p5位置,则必须能达到最高点,根据圆周运动的特点,能在竖直平面内做圆周运动需要条件,列圆周运动的向心力公式,结合受力特点即可求解第二问;
(3)根据法拉第电磁感应定律求出感应电动势,由闭合电路欧姆定律、电场公式联立方程即可解决第三问.
解答:解:(1)小滑块运动到位置p2时速度为v1,由动能定理有:
-umgL=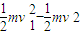
v1=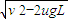
(2)由题意可知,电场方向如图,若小滑块能通过位置p,则小滑块可沿挡板运动且通过位置p5,设小滑块在位置p的速度为v,受到的挡板的弹力为N,
匀强电场的电场强度为E,由动能定理有: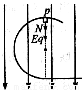
-umgL-2rEq=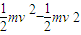
当滑块在位置p时,由牛顿第二定律有:mg+N+Eq=m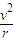
由题意有:N≥0
由以上三式可得:E≤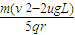
E的取值范围:0<E≤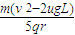 ①
①
(3)设线圈产生的电动势为E1,其电阻为R,平行板电容器两端的电压为U,t时间内磁感应强度的变化量为△B,得:
U=Ed ②
由法拉第电磁感应定律得E1=n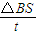 ③
③
由全电路的欧姆定律得E1=I(R+2R) ④
U=2RI ⑤
由②③④⑤得:△B=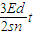
把①带入上式得:0<△B≤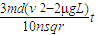
所以经过时间t,磁感应强度变化量的取值范围:0<△B≤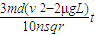 .
.
答:(1)小滑块通过p2位置时的速度大小为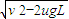 ;(2)电容器两极板间电场强度的取值范围为0<E≤
;(2)电容器两极板间电场强度的取值范围为0<E≤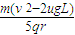 ;(3)经过时间t,磁感应强度变化量的取值范围为0<△B≤
;(3)经过时间t,磁感应强度变化量的取值范围为0<△B≤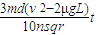 .
.
点评:对于这类题目,首先要细分过程,题目中条件繁杂,要画出特定条件下的轨迹图,要对每个过程进行受力分析,从而链接熟悉的题型,就像本题第二个过程,大体上属于圆周运动,再细分就类同于学过的竖直面内的非匀速圆周运动;此外一定要把所求问题和已知条件,特别是特定条件结合起来,寻求解题思路.就像第三问,求磁感应强度变化量,它所联系的是法拉第电磁感应定律,列出公式,转化为求E,再根据欧姆定律转化为求U,这样正反推导就可解决复杂问题.
(2)小滑块要能到达p5位置,则必须能达到最高点,根据圆周运动的特点,能在竖直平面内做圆周运动需要条件,列圆周运动的向心力公式,结合受力特点即可求解第二问;
(3)根据法拉第电磁感应定律求出感应电动势,由闭合电路欧姆定律、电场公式联立方程即可解决第三问.
解答:解:(1)小滑块运动到位置p2时速度为v1,由动能定理有:
-umgL=
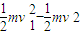
v1=
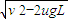
(2)由题意可知,电场方向如图,若小滑块能通过位置p,则小滑块可沿挡板运动且通过位置p5,设小滑块在位置p的速度为v,受到的挡板的弹力为N,
匀强电场的电场强度为E,由动能定理有:

-umgL-2rEq=
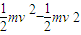
当滑块在位置p时,由牛顿第二定律有:mg+N+Eq=m
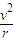
由题意有:N≥0
由以上三式可得:E≤
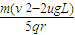
E的取值范围:0<E≤
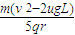 ①
①(3)设线圈产生的电动势为E1,其电阻为R,平行板电容器两端的电压为U,t时间内磁感应强度的变化量为△B,得:
U=Ed ②
由法拉第电磁感应定律得E1=n
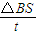 ③
③由全电路的欧姆定律得E1=I(R+2R) ④
U=2RI ⑤
由②③④⑤得:△B=
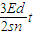
把①带入上式得:0<△B≤
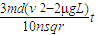
所以经过时间t,磁感应强度变化量的取值范围:0<△B≤
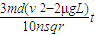 .
.答:(1)小滑块通过p2位置时的速度大小为
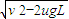 ;(2)电容器两极板间电场强度的取值范围为0<E≤
;(2)电容器两极板间电场强度的取值范围为0<E≤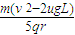 ;(3)经过时间t,磁感应强度变化量的取值范围为0<△B≤
;(3)经过时间t,磁感应强度变化量的取值范围为0<△B≤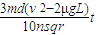 .
.点评:对于这类题目,首先要细分过程,题目中条件繁杂,要画出特定条件下的轨迹图,要对每个过程进行受力分析,从而链接熟悉的题型,就像本题第二个过程,大体上属于圆周运动,再细分就类同于学过的竖直面内的非匀速圆周运动;此外一定要把所求问题和已知条件,特别是特定条件结合起来,寻求解题思路.就像第三问,求磁感应强度变化量,它所联系的是法拉第电磁感应定律,列出公式,转化为求E,再根据欧姆定律转化为求U,这样正反推导就可解决复杂问题.

练习册系列答案
相关题目
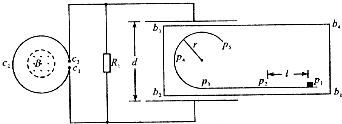 (2009?四川)如图所示,直线形挡板p1p2p3与半径为r的圆弧形挡板p3p4p5平滑连接并安装在水平台面b1b2b3b4上,挡板与台面均固定不动.线圈c1c2c3的匝数为n,其端点c1、c3通过导线分别与电阻R1和平行板电容器相连,电容器两极板间的距离为d,电阻R1的阻值是线圈c1c2c3阻值的2倍,其余电阻不计,线圈c1c2c3内有一面积为S、方向垂直于线圈平面向上的匀强磁场,磁场的磁感应强度B随时间均匀增大.质量为m的小滑块带正电,电荷量始终保持为q,在水平台面上以初速度v0从p1位置出发,沿挡板运动并通过p5位置.若电容器两板间的电场为匀强电场,p1、p2在电场外,间距为L,其间小滑块与台面的动摩擦因数为μ,其余部分的摩擦不计,重力加速度为g.
(2009?四川)如图所示,直线形挡板p1p2p3与半径为r的圆弧形挡板p3p4p5平滑连接并安装在水平台面b1b2b3b4上,挡板与台面均固定不动.线圈c1c2c3的匝数为n,其端点c1、c3通过导线分别与电阻R1和平行板电容器相连,电容器两极板间的距离为d,电阻R1的阻值是线圈c1c2c3阻值的2倍,其余电阻不计,线圈c1c2c3内有一面积为S、方向垂直于线圈平面向上的匀强磁场,磁场的磁感应强度B随时间均匀增大.质量为m的小滑块带正电,电荷量始终保持为q,在水平台面上以初速度v0从p1位置出发,沿挡板运动并通过p5位置.若电容器两板间的电场为匀强电场,p1、p2在电场外,间距为L,其间小滑块与台面的动摩擦因数为μ,其余部分的摩擦不计,重力加速度为g.