题目内容
如图，一“
”形绝缘导轨竖直放置，处在水平向右的匀强电场中。左边的半圆弧与水平杆ab、cd相切于a、c两点，两水平杆的高度差为h，杆长为4L，O为ad、bc连线的交点，虚线MN、M′N′的位置如图，其中aM = MM′= CN = NN′=L，M′b=N′d = 2L。一质量为m，带电量为－q的小球穿在杆上。虚线MN左边的导轨光滑，虚线MN右边的导轨与小球之间的动摩擦因数为
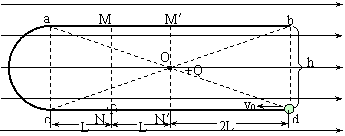
。已知：在O处没有固定点电荷+Q的时候，将带电小球自N点由静止释放后，小球刚好可到达a点。现在O处固定点电荷+Q，并将带电小球自d点以初速度v0向左瞬间推出。结果小球可沿杆运动到b点。（静电力恒量为k，重力加速度为g，在运动过程中+Q对-q的电场力始终小于小球的重力）求： （1）匀强电场的电场强度E；
（2）运动过程中小球所受摩擦力的最大值fm和小球经过M′点时的加速度大小a ；
（3）使小球能够运动到b点的初速度v0的最小值。
解：（1）由题意有：
∴
4分 （2）经分析可知：小球经过M′点时，球与轨道之间的弹力最大，所受的滑动摩擦力最大
4分小球经过M′点时的加速度大小为：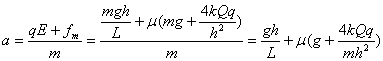
4分 （3）根据对称性可知，由d→b，小球克服摩擦力做的功等效为：
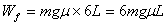而电场力做的功为零4分∴初速度v0的最小值应满足：
∴
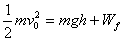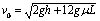4分
∴4分 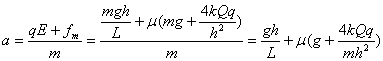（2）经分析可知：小球经过M′点时，球与轨道之间的弹力最大，所受的滑动摩擦力最大4分小球经过M′点时的加速度大小为：4分 （3）根据对称性可知，由d→b，小球克服摩擦力做的功等效为：而电场力做的功为零4分∴初速度v0的最小值应满足：∴4分 
练习册系列答案
相关题目
（2011?商丘二模）如图所示，将一根绝缘硬金属导线弯曲成一个完整的正弦曲线形状，它通过两个小金属环a、b与长直金属杆导通，在外力F作用下，正弦形金属线可以在杆上无摩擦滑动．杆的电阻不计，导线电阻为R，ab间距离为2L，导线组成的正弦图形项部或底部到杆距离都是
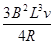
B．
C．
B．
C．
D．
B．
C．
D．