题目内容
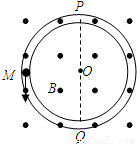
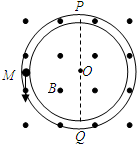 如图所示一半径为R=2.5m的内壁光滑绝缘的圆环竖直放置,环内有一质量为m=0.01kg、电荷量q=-0.2C的带电小球(可视为质点),在空间中存在竖直纸面向外的匀强磁场,磁感应强度为B=0.5T.图中虚线PQ为圆环竖直方向的一条直径.现让小球从与圆心O等高处的M点以某一初速度竖直向下开始运动,恰好能通过圆环的最高点P.求小球在最低点对圆环的压力大小及方向.
如图所示一半径为R=2.5m的内壁光滑绝缘的圆环竖直放置,环内有一质量为m=0.01kg、电荷量q=-0.2C的带电小球(可视为质点),在空间中存在竖直纸面向外的匀强磁场,磁感应强度为B=0.5T.图中虚线PQ为圆环竖直方向的一条直径.现让小球从与圆心O等高处的M点以某一初速度竖直向下开始运动,恰好能通过圆环的最高点P.求小球在最低点对圆环的压力大小及方向.分析:(1)小球恰好能通过圆环的最高点P,小球在P处的速度为0.
(2)小球在运动过程中只有重力做功,可应用动能定理解出在最低点的速度,对小球进行受力分析,找出向心力列式可求出支持力N,进而求出压力.
(2)小球在运动过程中只有重力做功,可应用动能定理解出在最低点的速度,对小球进行受力分析,找出向心力列式可求出支持力N,进而求出压力.
解答:解:依题意,恰好能通过圆环的最高点P,小球在P处的速度为0
设小球在Q处的初速度为v,到达最高点的过程中:
重力做功:-mg2R
初动能:
mv2,末动能:0
由动能定理:-mg2R=0-
mv2
解得:v=10m/s
小球在Q处,设环对小球的弹力竖直向上,由向心力公式及牛顿第二定律:
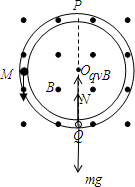
qvB+N-mg=m
解得:N=-0.5N
负号说明小球对环的作用力竖直向下,由牛顿第三定律:
小球在环的最低点时,对环的压力大小为0.5N,方向竖直向上.
答:小球在环的最低点时,对环的压力大小为0.5N,方向竖直向上.
设小球在Q处的初速度为v,到达最高点的过程中:
重力做功:-mg2R
初动能:
| 1 |
| 2 |
由动能定理:-mg2R=0-
| 1 |
| 2 |
解得:v=10m/s
小球在Q处,设环对小球的弹力竖直向上,由向心力公式及牛顿第二定律:

qvB+N-mg=m
| V2 |
| R |
解得:N=-0.5N
负号说明小球对环的作用力竖直向下,由牛顿第三定律:
小球在环的最低点时,对环的压力大小为0.5N,方向竖直向上.
答:小球在环的最低点时,对环的压力大小为0.5N,方向竖直向上.
点评:带电粒子在电磁场中的运动一般有直线运动、圆周运动和一般的曲线运动;直线运动一般由动力学公式求解,圆周运动由洛仑兹力充当向心力,一般的曲线运动一般由动能定理求解.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 (2011?西乡县模拟)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的AB及其以下部分处于向左的匀强电场中,管的内壁光滑,现将一质量为m,带电量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )
(2011?西乡县模拟)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的AB及其以下部分处于向左的匀强电场中,管的内壁光滑,现将一质量为m,带电量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )