题目内容
【题目】劲度系数为k的轻弹簧,一端系在竖直放置、半径为R的光滑圆环顶点P,另一端连接一套在圆环上且质量为m的小球,开始时小球位于A点,此时弹簧处于原长且与竖直方向的夹角为45°,之后小球由静止沿圆环下滑,小球运动到最低点B时速率为v,此时小球与圆环间弹力恰好为零。当地重力加速度取g,则正确的说法是
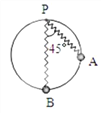
A. 小球经过B点时,弹簧的弹力大小为![]()
B. 小球经过B点时,弹簧的弹力大小为![]()
C. 从A到B的过程中,小球减少的重力势能全部转化为弹簧的弹性势能
D. 从A到B的过程中,重力对小球做的功等于小球克服弹簧弹力做的功
【答案】ACD
【解析】试题分析:小球运动到最低点B时速率为v,此时小球与圆环之间压力恰好为零,此时小球受重力、弹簧的弹力,由题意可知弹簧的弹力与重力的合力恰好提供小球所需要的向心力.则:![]() ,所以小球过B点时,弹簧的弹力大小为:
,所以小球过B点时,弹簧的弹力大小为:![]() ,故A正确;小球过B点时,弹簧的伸长量:
,故A正确;小球过B点时,弹簧的伸长量:![]() ,则弹力大小为
,则弹力大小为![]() ,故B正确;从A到B的过程中,小球的重力势能减小,动能增大,则知重力势能转化为小球的动能和弹簧的弹性势能.故C正确;从A到B的过程中,重力做正功,弹簧的弹力做负功,由于动能增大,由动能定理知,总功为正,所以重力对小球做的功大于小球克服弹簧弹力做的功.故D错误.所以ABC正确,D错误。
,故B正确;从A到B的过程中,小球的重力势能减小,动能增大,则知重力势能转化为小球的动能和弹簧的弹性势能.故C正确;从A到B的过程中,重力做正功,弹簧的弹力做负功,由于动能增大,由动能定理知,总功为正,所以重力对小球做的功大于小球克服弹簧弹力做的功.故D错误.所以ABC正确,D错误。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目