��Ŀ����
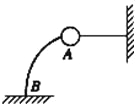
����Ŀ����ͼ��ʾ,һ������Ϊ0.6kg��С����ijһ���ٶȴ�P��ˮƽ�׳�,ǡ�ô�Բ��ABC��A������߷������Բ��(���ƿ�������,����Բ��ʱ��������ʧ)����֪Բ���İ뾶R=0.6m, ![]() =60��,С��A��ʱ���ٶ�vA=8m/s��gȡ10m/s2,��:
=60��,С��A��ʱ���ٶ�vA=8m/s��gȡ10m/s2,��:

(1)С����ƽ���˶��ij��ٶ�v0
(2)P����A��ĸ߶Ȳ�
(3)С��պ��ܵ���Բ����ߵ�C,��˹���С��˷�Ħ���������Ĺ���
���𰸡���1��4 m/s��2��2.4 m��3��12J
��������(1)������֪С��A����ٶ�vA��������A������߷����ٶȷֽ���ͼ��ʾ��
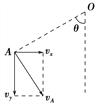
С����ƽ���˶�����ƽ���˶����ɵã�v0��vx��vAcos ����4 m/s
(2)С����P��A�Ĺ����ɶ��ܶ����ã�
mgh��![]() mvA2��
mvA2��![]() mv02
mv02
��ã�h��2.4 m
(3)С��ǡ�þ���C��ʱ����C����ţ�ٵڶ����ɵã�
mg��m![]()
��ã�vC��![]() m/s
m/s
С����A��C�����ɶ��ܶ����ã���mg(Rcos ����R)��Wf��![]() mvC2��
mvC2��![]() mvA2
mvA2
��ã�Wf��12J

��ϰ��ϵ�д�
�����Ŀ