题目内容
【题目】如图所示，两个相同的小球A、B用长度分别为l1、l2的细线（l1<l2）悬于天花板上的O1、O2点，两球在水平面内做匀速圆周运动，两根细线与竖直轴夹角均为θ。设A、B两球的线速度分别为v1、v2，角速度分别为ω1、ω2，加速度分别为a1、a2，两根细线的拉力分别为F1、F2，则（）
A. 
B. 
C. 
D. 
【答案】BC
【解析】小球在水平面内做匀速圆周运动，对小球受力分析，如图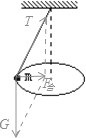
小球受重力、和绳子的拉力，合力提供向心力，根据几何关系可知向心力：F=mgtanθ；由向心力公式得： 
；又 r=lsinθ
解得： 
由于l1＜l2，所以vA＜vB．故A D错误；
由于v=ωr=ωlsinθ，故角速度： 
，由于l1＜l2，所以ω1＞ω2．故B正确；由向心力公式得：mgtanθ=ma，所以二者的加速度是相等的．故C正确；
故选BC．
练习册系列答案
应用题作业本系列答案
相关题目
