题目内容
【题目】如图所示，带有足够高光滑弧形轨道的小车质量为M，放在光滑水平面上，一质量为m的小球，以速度v沿轨道水平端向上滑去，至某一高度后再向下返回，则当小球回到小车右端时( )
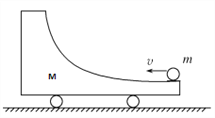
A. 小球可能做自由落体运动
B. 小球可能向右做平抛运动
C. 小球在弧形槽内上升的最大高度为
D. 此过程小球对小车做的功可能为
mv2
【答案】ABD
【解析】小球上升到最高点时与小车相对静止，有共同速度
，规定向左为正方向，由水平动量守恒得： 
，由机械能守恒定律得： 
， 联立解得： 
；小球在返回小车右端时速度为
，此时小车速度
，规定向左为正方向，由动量守恒定律可得： 
，由机械能守恒得： 
，联立解得： 
， 
；由
可知，若
，则
，小球将做自由落体运动，若
，则
，则小球将向右做平抛运动；若
，则
，由动能定理可得：小球对小车做的功为
，故ABD正确，C错误；故选ABD.
练习册系列答案
相关题目
【题目】在探究小车速度随时间变化规律的实验中，得到一条记录小车运动情况的纸带，如图所示。图中A、B、C、D、E为相邻的计数点，相邻计数点的时间间隔为T＝0.1s。
（1）根据纸带上的数据，计算B、C、D各点的速度，填入表中__________；_________；__________。
位置编号 | A | B | C | D | E |
时间t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
瞬时速度v/(m·s－1) |
（2）在坐标纸上作出小车的v－t图像________。并根据图象求出a＝____________。
（3）分析小车的速度随时间的变化规律_______________。
（4）将图线延长与纵轴相交，交点的速度是__________，此速度的物理意义是________________。E点的速度为_____________