��Ŀ����
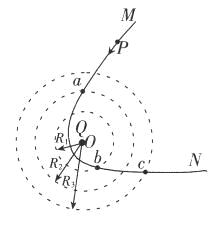
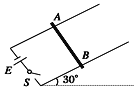
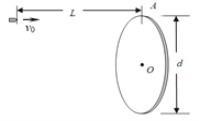
����Ŀ����ͼ��ʾ��AMN��DEF�ǹ̶��Ĺ⻬ƽ�н������죬���ΪlAM��DE����ˮƽ��н�Ϊ�������ڷ���ֱ�������ϵĴų��С�MN��EF��ˮƽ��������ֱ���ϵ���ǿ�ų��У�������һ��ֹ������b������Ϊm2����NF���Ҳ࣬�⻬��ˮƽ��������һ������Ϊm3�ı�ľ�忿�ŵ���ĩ�ˣ��ϱ����뵼��MNEF��ƽ���뵼����b֮��Ħ������Ϊ�����ڵ�����и�����ΪC�ĵ�������һ������˫������K����ֵ����R����ʼ�����������磬K����1�ˡ��ڵ���AMDE�϶��ɾ�ֹ�ͷ�һ������Ϊm1�ĵ����a������һ��ʱ����������б�����������˶�����֪�����ų��ĴŸ�Ӧǿ�ȴ�С��ΪB������a��b�ĵ�����Բ��ƣ�����b�Ŀ��Ȳ��ơ���
(1)���������б�����������˶����ٶ�v1��
(2)���������б�����������˶�ʱ���������Ĵ�����Q��
(3)��a�����ٺ���K��1������2�˵�����b��һ���ٶȳ���ľ�壬��û�д�ľ���ϻ��£���ʱ���������˵�ѹΪU����ľ�峤�ȵ���Сֵ��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
��1��������������˶�ʱ������б�����µķ������ڰ���������ʽ����ٶȣ���2�������˶�ʱ��������û�е��������˵�ѹΪ�綯�ƣ�����q=CE������������������3������K��1������2�˵�����b��һ���ٶȳ���ľ�壬���ݶ���������ϰ������ij�������ٶȣ����ݶ����غ㶨�ɺ�������ϵ���ľ����С����.
��1��a�������˶�ʱ�����ĵ綯��ΪE=Blv1��
����I=E/R
������F=BIl
��Ϊ�����˶���m1gsin��-F=0
���![]()
��2�������˶�ʱ��������û�е��������˵�ѹΪ�綯��q=CE��
���![]()
��3����b�ɶ������ɣ�I��=m2v2����![]()
![]()
���![]()
��b����ƽ����٣��ɶ����غ㶨�ɣ�![]()
��ʧ�Ķ���![]()
��ʧ�Ķ���ת��ΪĦ������![]() ����LΪľ�����С���ȣ�f=��m2g��
����LΪľ�����С���ȣ�f=��m2g��
���![]()

 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�