题目内容
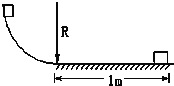
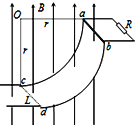
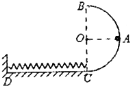
【题目】如图所示，光滑半圆弧形轨道半径为r=0.4m，BC为竖直直径，A为半圆弧形轨道上与圆心O等高的位置．一质量为m=2.0kg的小球（可视为质点）自A处以某一竖直向下的初速度滑下，进入与C点相切的粗糙水平面CD上，在水平滑道上有一轻质弹簧，其一端固定在竖直墙上，另一端位于滑道末端的C点（此时弹簧处于自然状态．若小球与水平滑道间的动摩擦因数为μ=0.5，弹簧被压缩的最大长度为0.2m．小球经弹簧反弹后恰好能通过半圆弧形轨道的最高点B，重力加速度g=lOm/s2．则下列说法中正确的是（ ）
A. 小球通过最高点B时的速度大小为2m/s
B. 小球运动过程中弹簧的最大弹性势能为20J
C. 小球第一次经过C点时对C点的压力为120N
D. 小球从A点竖直下滑的初速度大小为4m/s
【答案】A
【解析】
试题小球被轻弹簧反弹后恰好能通过半圆形轨道的最高点B，故在B点是重力提供向心力，故：
解得：
故A正确；对反弹后到最高点的过程根据动能定理，有：W弹μmgx mg（2R）=
mv20；其中：W弹=Epm；
联立解得：Epm=μmgx+mg（2r）+mv2=0.5×2×10×0.2+2×10×（2×0.4）+×2×22=22J；故B错误；
从A到C，根据动能定理，有：
解得：
；在C点，根据牛顿第二定律，有：
；解得：
故C错误；对运动全程，根据动能定理，有：
，解得：
，故D正确；故选AD.
练习册系列答案
阅读快车系列答案
相关题目
