题目内容
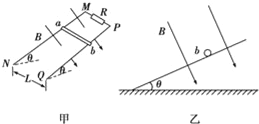
【题目】如图所示,半径为a的圆内有一固定的边长为1.5a的等边三角形框架ABC,框架中心与圆心重合,S为位于BC边中点处的狭缝.三角形框架内有一水平放置带电的平行金属板,框架与圆之间存在磁感应强度大小为B,方向垂直纸面向里的匀强磁场.一束质量为m、电量为q,不计重力的带正电的粒子,从P点由静止经两板间电场加速后通过狭缝S,垂直BC边向下进入磁场并发生偏转.忽略粒子与框架碰撞时能量与电量损失.求:
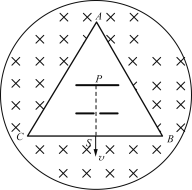
(1)要使粒子进入磁场后第一次打在SB的中点,则加速电场的电压为多大?
(2)要使粒子最终仍能回到狭缝S,则加速电场电压满足什么条件?
(3)回到狭缝S的粒子在磁场中运动的最短时间是多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)带电粒子在匀强电场中做匀加速直线运动,进入磁场后做圆周运动,结合几何关系找到半径,求解加速电场的电压;(2)要使粒子能回到S,则每次碰撞时粒子速度都应与边垂直,则可能的情况是:粒子与框架垂直碰撞,绕过三角形顶点时的轨迹圆弧的圆心应位于三角形顶点上,即SB为半径的奇数倍;要使粒子能绕过顶点且不飞出磁场,临界情况为粒子轨迹圆与磁场区域圆相切;(3)根据带电粒子在磁场中做匀速圆周运动的轨迹图,找到圆周运动的圆心角,结合圆周运动周期公式,求出在磁场中运动的最短时间;
(1)粒子在电场中加速,qU=![]() mv2
mv2
粒子在磁场中,qvB=![]()
r=![]()
解得![]()
(2)要使粒子能回到S,则每次碰撞时粒子速度都应与边垂直,则r和v应满足以下条件:
①粒子与框架垂直碰撞,绕过三角形顶点时的轨迹圆弧的圆心应位于三角形顶点上,即SB为半径的奇数倍,
即![]() (n=1,2,3,… )
(n=1,2,3,… )
②要使粒子能绕过顶点且不飞出磁场,临界情况为粒子轨迹圆与磁场区域圆相切,
即r≤a-![]() a
a
解得n≥3.3,即n=4,5,6…
得加速电压![]() (n=4,5,6,…).
(n=4,5,6,…).
(3)粒子在磁场中运动周期为T
qvB=![]() ,T=
,T=![]()
解得T=![]()
当n=4时,时间最短,即 tmin=3×6×![]() +3×
+3×![]() T=
T=![]() T
T
解得tmin=![]() .
.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案