题目内容
9. 一同学用图示装置研究色散现象,半径为R的半圆形玻璃砖下端紧靠在足够大的EF上.O点为圆心,OO′为直径PQ的垂线.一束复色光沿半径方向与OO′成θ=30°角射向O点.已知复色光包含有折射率从n1=$\sqrt{2}$到n2=1.6的光束,光屏上出现了彩色光带.sin37°=0.6.
一同学用图示装置研究色散现象,半径为R的半圆形玻璃砖下端紧靠在足够大的EF上.O点为圆心,OO′为直径PQ的垂线.一束复色光沿半径方向与OO′成θ=30°角射向O点.已知复色光包含有折射率从n1=$\sqrt{2}$到n2=1.6的光束,光屏上出现了彩色光带.sin37°=0.6.(1)求彩色光带的宽度L;
(2)改变复色光入射角,光屏上的彩色光带将变成一个光点,求此时的入射角.
分析 (1)两束光通过玻璃砖时,由于折射率不同,折射角不同,从而产生色散,根据折射定律求出折射角,由几何知识求解L.
(2)改变复色光入射角,光屏上的彩色光带将变成一个光点,说明临界角较小的光束发生了全反射,由sinC=$\frac{1}{n}$求解.
解答  解:(1)根据折射定律有:
解:(1)根据折射定律有:
n1=$\frac{sin{r}_{1}}{sinθ}$
n2=$\frac{sin{r}_{2}}{sinθ}$
可得 r1=45°,r2=53°
故彩色光带的宽度 L=Rcotr1-Rcotr2=0.25R
(2)根据sinC=$\frac{1}{n}$,知折射率为n2=1.6的光束全反射临界角较小,改变复色光入射角,光屏上的彩色光带将变成一个光点时,该光束发生了全反射,由sinC=$\frac{1}{{n}_{2}}$得
C=arcsin$\frac{5}{8}$
答:
(1)彩色光带的宽度L是0.25R;
(2)改变复色光入射角,光屏上的彩色光带将变成一个光点,此时的入射角为arcsin$\frac{5}{8}$.
点评 对于涉及全反射的问题,要紧扣全反射产生的条件:一是光从光密介质射入光疏介质;二是入射角大于临界角.

练习册系列答案
相关题目
19.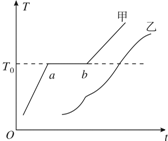 固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
 固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )
固体甲和固体乙在一定压强下的熔解曲线如图所示,横轴表示时间t,纵轴表示温度T.下列判断正确的有 ( )| A. | 固体甲一定是晶体,固体乙一定是非晶体 | |
| B. | 固体甲不一定有确定的几何外形,固体乙一定没有确定的几何外形 | |
| C. | 在热传导方面固体甲一定表现出各向异性,固体乙一定表现出各向同性 | |
| D. | 固体甲和固体乙的化学成分有可能相同 | |
| E. | 图线甲中ab段温度不变,所以甲的内能不变 |
4. 在边长为L、电阻为R的正方形导线框内,以对称轴ab为界,左、右两侧分别存在着方向如图甲所示的匀强磁场.以垂直纸面向外的磁场为正,两部分磁场的感应强度B随时间t的变化规律分别如图乙所示.则在0-t0时间内,导线框中( )
在边长为L、电阻为R的正方形导线框内,以对称轴ab为界,左、右两侧分别存在着方向如图甲所示的匀强磁场.以垂直纸面向外的磁场为正,两部分磁场的感应强度B随时间t的变化规律分别如图乙所示.则在0-t0时间内,导线框中( )
 在边长为L、电阻为R的正方形导线框内,以对称轴ab为界,左、右两侧分别存在着方向如图甲所示的匀强磁场.以垂直纸面向外的磁场为正,两部分磁场的感应强度B随时间t的变化规律分别如图乙所示.则在0-t0时间内,导线框中( )
在边长为L、电阻为R的正方形导线框内,以对称轴ab为界,左、右两侧分别存在着方向如图甲所示的匀强磁场.以垂直纸面向外的磁场为正,两部分磁场的感应强度B随时间t的变化规律分别如图乙所示.则在0-t0时间内,导线框中( )| A. | 无感应电流 | |
| B. | 感应电流逐渐变大 | |
| C. | 感应电流为顺时针方向,大小为$\frac{{{L^2}{B_0}}}{{{t_0}R}}$ | |
| D. | 感应电流为逆时针方向,大小为$\frac{{2{L^2}{B_0}}}{{{t_0}R}}$ |
1.下列叙述正确的有( )
| A. | β衰变现象说明电子是原子核的组成部分 | |
| B. | 目前已建成的核电站的能量来自于重核裂变 | |
| C. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能增大,原子总能量增大 | |
| D. | 卢瑟福依据极少数α粒子发生大角度散射提出了原子核式结构模型 |
19. 如图所示,斜面体ABC放在水平桌面上,其倾角为37°,其质量为M=5kg.现将一质量为m=3kg的小物块放在斜面上,并给予其一定的初速度让其沿斜面向上或者向下滑动.已知斜面体ABC并没有发生运动,重力加速度为10m/s2,sin37°=0.6.则关于斜面体ABC受到地面的支持力N及摩擦力f的大小,下面给出的结果可能的有( )
如图所示,斜面体ABC放在水平桌面上,其倾角为37°,其质量为M=5kg.现将一质量为m=3kg的小物块放在斜面上,并给予其一定的初速度让其沿斜面向上或者向下滑动.已知斜面体ABC并没有发生运动,重力加速度为10m/s2,sin37°=0.6.则关于斜面体ABC受到地面的支持力N及摩擦力f的大小,下面给出的结果可能的有( )
 如图所示,斜面体ABC放在水平桌面上,其倾角为37°,其质量为M=5kg.现将一质量为m=3kg的小物块放在斜面上,并给予其一定的初速度让其沿斜面向上或者向下滑动.已知斜面体ABC并没有发生运动,重力加速度为10m/s2,sin37°=0.6.则关于斜面体ABC受到地面的支持力N及摩擦力f的大小,下面给出的结果可能的有( )
如图所示,斜面体ABC放在水平桌面上,其倾角为37°,其质量为M=5kg.现将一质量为m=3kg的小物块放在斜面上,并给予其一定的初速度让其沿斜面向上或者向下滑动.已知斜面体ABC并没有发生运动,重力加速度为10m/s2,sin37°=0.6.则关于斜面体ABC受到地面的支持力N及摩擦力f的大小,下面给出的结果可能的有( )| A. | N=50N,f=40N | B. | N=87.2N,f=9.6N | C. | N=72.8N,f=0N | D. | N=77N,f=4N |

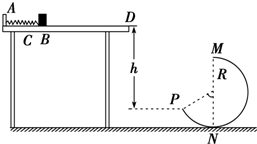 如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.水平桌面右侧有一竖直放置的轨道MNP,其形状为半径R=1.0m的圆环剪去了左上角120°的圆弧,MN为其竖直直径,P点到桌面的竖直距离是h=2.4m.用质量为m=0.2kg的物块将弹簧缓慢压缩到C点后释放,物块过B点后做匀变速运动,其位移与时间的关系为s=6t-2t2(m),物块飞离桌面后恰好由P点沿切线落入圆轨道.(不计空气阻力,g取10m/s2)
如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.水平桌面右侧有一竖直放置的轨道MNP,其形状为半径R=1.0m的圆环剪去了左上角120°的圆弧,MN为其竖直直径,P点到桌面的竖直距离是h=2.4m.用质量为m=0.2kg的物块将弹簧缓慢压缩到C点后释放,物块过B点后做匀变速运动,其位移与时间的关系为s=6t-2t2(m),物块飞离桌面后恰好由P点沿切线落入圆轨道.(不计空气阻力,g取10m/s2) 如图甲所示,圆形的刚性金属线圈与一平行板电容器连接,线圈内存在垂直于线圈平面的匀强磁场,取垂直于纸面向里为磁感应强度B的正方向,B随时间t的变化关系如图乙所示.t=0时刻,在平行板电容器间,由静止释放一带正电的粒子(重力可忽略不计),假设粒子运动未碰到极板,不计线圈内部磁场变化对外部空间的影响,下列关于粒子在板间运动的速度图象和位移图象(以向上为正方向)正确的是( )
如图甲所示,圆形的刚性金属线圈与一平行板电容器连接,线圈内存在垂直于线圈平面的匀强磁场,取垂直于纸面向里为磁感应强度B的正方向,B随时间t的变化关系如图乙所示.t=0时刻,在平行板电容器间,由静止释放一带正电的粒子(重力可忽略不计),假设粒子运动未碰到极板,不计线圈内部磁场变化对外部空间的影响,下列关于粒子在板间运动的速度图象和位移图象(以向上为正方向)正确的是( )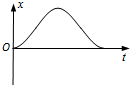


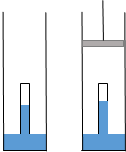 在一个可以插入活塞的圆筒内装置着著名的托里拆利实验结构,由于操作不慎,管内混入少量气体,结果水银柱的高度如图A所示上方空气柱长度30cm,下方水银60cm,此时 大气压强为75cmHg,求:
在一个可以插入活塞的圆筒内装置着著名的托里拆利实验结构,由于操作不慎,管内混入少量气体,结果水银柱的高度如图A所示上方空气柱长度30cm,下方水银60cm,此时 大气压强为75cmHg,求: