题目内容
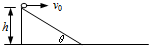如图所示，一个斜面固定在水平面上，从斜面顶端以不同初速度v0水平抛出小物体，得到物体在空中运动时间t与初速度v0的关系如表，试求：| v0m．s-1 | … | 2 | … | 9 | 10 | … |
| t/s | … | 0.250 | … | 1.000 | 1.000 | … |
（2）斜面的倾角θ
分析：（1）从表格可知，当速度大于等于9m/s时，下落的时间不变，因为平抛运动的高度决定运动的时间，知物体落在水平面上，结合运动时间求出斜面的高度．
（2）当速度为2m/s时，物体落在斜面上，抓住竖直位移和水平位移的关系求出斜面的倾角．
（2）当速度为2m/s时，物体落在斜面上，抓住竖直位移和水平位移的关系求出斜面的倾角．
解答：（1）因为初速度达到9m/s以后运动时间保持1s不变，故小物体落地点在水平面
h=
gt2=
×10×1m=5m
（2）小物体初速度2m/s，运动时间0.250s时落在斜面
tanθ=
=
=0.625
解得θ=32°
答：（1）斜面的高度为5m．
（2）斜面的倾角为32°．
h=
| 1 |
| 2 |
| 1 |
| 2 |
（2）小物体初速度2m/s，运动时间0.250s时落在斜面
tanθ=
| ||
| v0t |
| gt |
| 2v0 |
解得θ=32°
答：（1）斜面的高度为5m．
（2）斜面的倾角为32°．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式灵活求解．
练习册系列答案
相关题目
为了测量小木板和斜面间的动摩擦因数，某同学设计了如下的实验．在小木板上固定一个弹簧秤（弹簧秤的质量可不计），弹簧秤下吊一个光滑小球．将木板连同小球一起放在斜面上．如图所示，木板固定时，弹簧秤的示数为F1，放手后木板沿斜面下滑，稳定时弹簧秤的示数是F2，测得斜面的倾角为θ．由测量的数据可以计算出小木板跟斜面间动摩擦因数为
如图所示，光滑的斜面上有一个小物块，当斜面固定时，它下滑的加速度为a1；当用一个水平力推动斜面，使斜面与小物块在水平面上共同加速而二者又保持相对静止时加速度为a2．则两次加速度的大小之比a1：a2为（ ）
一斜面固定在水平面上，在斜面顶端有一长木板，木板与斜面之间的动摩擦因数为?，木板上固定一轻质弹簧测力计，弹簧测力计下面固定一个光滑的小球如图所示，木板固定时，弹簧测力计示数为F1，由静止释放后木板沿斜面下滑，稳定时弹簧测力计的示数为F2，斜面的高为h，底边长为d，则下列说法正确的是（ ）
