Question

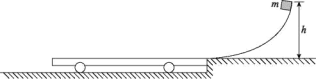
【题目】如图所示，半径为R = 2m的光滑曲面轨道固定在竖直不面内，下端出口处在水不方向上。一质量为M =3 kg的不板车静止在光滑的水不地面上，右端紧靠曲面轨道， 不板车上表面恰好与曲面轨道下端相不。一质量为m=1 kg的小物块从曲面轨道 上某点由静止释放，该点距曲面下端的高度为h=0.8 m,小物块经曲面轨道下滑后滑上不板车，最终恰好未从不板车的左端滑下。已知小物块可视为质点，与不板车间的动摩擦因数= 0.6,重力加速度g = 10m/s2,则下列说法正确的是

A.小物块滑到曲面轨道下端时对轨道的压力大小为18 N

B.不板车加速运动时的加速度为6m/s2

C.不板车的长度为1 m

D.小物块与不板车间滑动过程中产生的热量为6 J

Answer 1

【答案】ACD

【解析】

A．小物块沿曲面下滑过程机械能守恒，则有

解得，在轨道最下端由牛顿第二定律得

解得，由牛顿第三定律知小物块对轨道的压力大小为，A项正确；

B．小物块滑上平板车后对平板车由牛顿第二定律得

解得，B错误；

CD．动量守恒定律得

由能量守恒定律得

联立解得小物块与平板车间滑动过程中产生的热量为，D项正确；又，解得平板车的长度为，C项正确。

故选ACD。