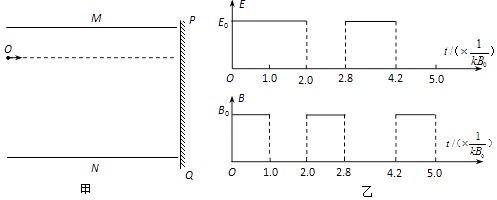
题目内容
【题目】如图所示,MN为竖直放置的光屏,光屏的左侧有半径为R、折射率为 ![]() 的透明半球体,O为球心,轴线OA垂直于光屏,O至光屏的距离OA=
的透明半球体,O为球心,轴线OA垂直于光屏,O至光屏的距离OA= ![]() R.一细束单色光垂直射向半球体的平面,在平面的入射点为B,OB=
R.一细束单色光垂直射向半球体的平面,在平面的入射点为B,OB= ![]() R求:
R求: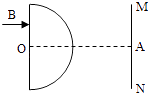
(1)光线从透明半球体射出时,出射光线偏离原方向的角度.
(2)光线在光屏形成的光斑到A点的距离.
【答案】
(1)
解:分析如图.设入射点B到O的垂直距离BO=h,∠BCO=β,折射角为i.

对△OBC,由正弦公式得: ![]()
又 ![]()
联立解得 ![]()
所以:i=60°
出射光线偏离原方向的角度:△θ=i﹣β=60°﹣30°=30°
(2)
解:设出射光线与MN交与P点,与OA交与D点,则由几何关系可得,∠CDQ=30°
所以: ![]()
![]()
所以: ![]() =0.5R
=0.5R
【解析】(1)根据数学上正弦定理和折射定律分别列式,得到∠BOA,即可求得出射光线偏离原方向的角度.(2)光线在光屏形成的光斑到A点的距离.
【考点精析】根据题目的已知条件,利用光的折射的相关知识可以得到问题的答案,需要掌握光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目