题目内容
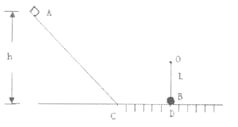
【题目】如图所示,光滑斜面与水平地面在C点平滑连接,质量为0.4kg的滑块A无初速地沿斜面滑下后,又沿水平地面运动至D点与质量也为0.4kg的小球B发生正碰,碰撞时没有机械能损失,小球B用长为L=0.32m的细绳悬于O点,其下端恰好与水平地面上的D点相切,已知滑块与水平地面间的动摩擦因素为μ=0.1,C、D间距L CD =1.4m,碰后B球恰好能在竖直平面内做完整的圆周运动,g=l0m/s 2 ,求:
(1)B球碰后的速度;
(2)滑块A在斜面上滑下时的高度h;
(3)滑块A最终与D点间的距离S。
【答案】(1)4m/s (2)0.94m (3)8m
【解析】
试题分析:(1)设A和B碰后B的速度为vB,对于B从最低点到最高点的过程,由机械能守恒得:
![]() mvB2=mg2L+
mvB2=mg2L+![]() mv2最高
mv2最高
在最高点,对B由牛顿第二定律得:![]()
解得:![]()
(2)设A与B碰前、碰后速度分别为vD和vB′
根据动量守恒定律得:mvD=mvD′+mvB
根据机械能守恒定律得:![]() mvD′2=
mvD′2=![]() mvD2+
mvD2+![]() mvB2
mvB2
联立两式解得:vB=vD=4m/s,vD′=0
对A从C到D的过程,由动能定理得:μmgLCD=![]() mv2-
mv2-![]() mvD2
mvD2
下滑过程,有:Mgh=![]() mvC2
mvC2
解得:h=0.94m
(3)设滑块A最终与A的距离为S,由动能定理得:μmgS=![]() mvD2
mvD2
解得:S=8m

练习册系列答案
相关题目