题目内容
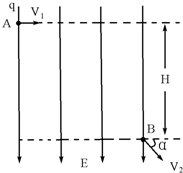
空间某区域存在竖直向下的匀强电场,电场线分布如图所示,带电小球质量为m,电量为q,在A点速度为v1,方向水平向右,至B点速度为v2,v2与水平方向的夹角为α,A、B间高度差为H,以下判断正确的是( )
A.A、B两点间电势差U=(
| ||||
B.小球由A至B,电场力做的功为
| ||||
C.电势能的减少量为
| ||||
| D.小球的重力在B点的即时功率为mgv2 |

A、小球由A至B,由动能定理得:mgH+qUAB=
m
-
m
,得A、B两点间电势差:UAB=
(
m
-
m
-mgH).故A错误.
B、由上式知,电场力做的功为:W=qUAB=
m
-
m
-mgH,故B正确.
C、电场力做功多少,电势能就减小多少,则知电势能的减少量为△E =
m
-
m
-mgH,故C错误.
D、小球的重力在B点的瞬时功率为mgv2sinα.故D错误.
故选:C
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| q |
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | 21 |
B、由上式知,电场力做的功为:W=qUAB=
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | 21 |
C、电场力做功多少,电势能就减小多少,则知电势能的减少量为△E =
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
| v | 21 |
D、小球的重力在B点的瞬时功率为mgv2sinα.故D错误.
故选:C

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
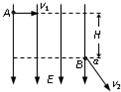 如图所示,空间某区域存在竖直向下的匀强电场.带电小球质量为m,电量为q,在A点以水平向右的速度为v1射入电场,到B点时速度为v2,与水平方向的夹角为α.A、B间的高度差为H.以下判断错误的是( )
如图所示,空间某区域存在竖直向下的匀强电场.带电小球质量为m,电量为q,在A点以水平向右的速度为v1射入电场,到B点时速度为v2,与水平方向的夹角为α.A、B间的高度差为H.以下判断错误的是( )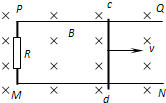 如图所示,空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T.在磁场区域内有两根相距L=0.50m的平行金属导轨PQ、MN固定在竖直平面内,PM间连接有R=5.0Ω的电阻.当导体棒cd沿导轨平面向右匀速运动时,在闭合回路中产生的电流I=0.20A.求:
如图所示,空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T.在磁场区域内有两根相距L=0.50m的平行金属导轨PQ、MN固定在竖直平面内,PM间连接有R=5.0Ω的电阻.当导体棒cd沿导轨平面向右匀速运动时,在闭合回路中产生的电流I=0.20A.求: (2006?和平区模拟)空间某区域存在竖直向下的匀强电场,电场线分布如图所示,带电小球质量为m,电量为q,在A点速度为v1,方向水平向右,至B点速度为v2,v2与水平方向的夹角为α,A、B间高度差为H,以下判断正确的是( )
(2006?和平区模拟)空间某区域存在竖直向下的匀强电场,电场线分布如图所示,带电小球质量为m,电量为q,在A点速度为v1,方向水平向右,至B点速度为v2,v2与水平方向的夹角为α,A、B间高度差为H,以下判断正确的是( )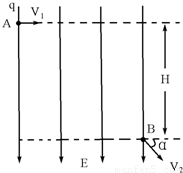
 mv22-
mv22- mv12)/q
mv12)/q mv22-
mv22- mv12-mgH
mv12-mgH mv22-
mv22- mv12
mv12