题目内容
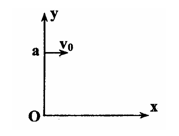
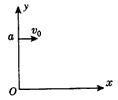
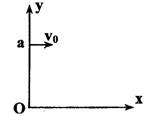
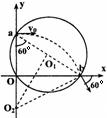
如图所示,a点距坐标原点的距离为l,坐标平面内有边界过a点和坐标原点o的圆形匀强磁场区域,磁场方向于垂直坐标平面向里.有一电子(质量为m、电荷量为e)从a点以初速度v0平行x轴正方向射入磁场区域,在磁场中运行,从x轴上的b点(图中未画出)射出磁场区域,此时速度方向与x轴的正方向之间的夹角为60°,求:
⑴ 磁场的磁感应强度大小;
⑵ 磁场区域的圆心o1的坐标;
⑶ 电子在磁场中运动的时间t。
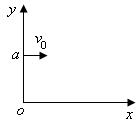
(1) mv0/2el (2) 坐标(![]() )(3) πl/3v0
)(3) πl/3v0
解析:
⑴ 由轨迹图可知R = 2l,根据牛顿第二定律有:eBv0 = mv02/R,
得B = mv0/2el。
⑵ 由轨迹图可知,x轴坐标 x = ao1sin600 = ![]() l,
l,
y轴坐标y = l – ao1sin600 = l/2,磁场圆心坐标(![]() )。
)。
⑶ 粒子在磁场中飞行时间为 t = T/6 = πl/3v0。

练习册系列答案
相关题目
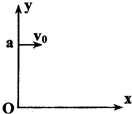 如图所示,a点距坐标原点的距离为L,坐标平面内有边界过a点和坐标原点0的圆形匀强磁场区域,磁场方向垂直坐标平面向里.有一电子(质量为m、电荷量为e)从a点以初速度v0平行x轴正方向射入磁场区域,在磁场中运行,从x轴上的b点(图中未画出)射出磁场区域,此时速度方向与x轴的正方向之间的夹角为60°,求
如图所示,a点距坐标原点的距离为L,坐标平面内有边界过a点和坐标原点0的圆形匀强磁场区域,磁场方向垂直坐标平面向里.有一电子(质量为m、电荷量为e)从a点以初速度v0平行x轴正方向射入磁场区域,在磁场中运行,从x轴上的b点(图中未画出)射出磁场区域,此时速度方向与x轴的正方向之间的夹角为60°,求